Techniklexikon

Bohrsche Theorie

Theorie des Atombaus und der Natur der Spektrallinien (Atomhülle), die 1913 von Bohr aufgestellt wurde, um die Inkonsistenzen des Rutherfordschen Atommodells (Atommodelle) mit der klassischen Elektrodynamik zu umgehen. Gemäss dem Rutherfordschen Modell besteht das Atom aus einem als punktförmig angenommenen, positiv geladenen Kern, in dessen elektrostatischem Feld sich die Elektronen bewegen. Klassisch gesehen, müssten die Elektronen bei ihrer Bewegung um den Kern elektromagnetische Strahlung abgeben, so dass sie kontinuierlich kinetische Energie verlieren und schliesslich in den Atomkern stürzen. Bohr beseitigte diese Inkonsistenzen dadurch, dass er die Existenz stabiler Zustände der Elektronen im Atom ad hoc postulierte. Die Bohrsche Theorie erweiterte das Rutherfordsche Modell durch heuristische Annahmen (Bohrsche Postulate):

a) Bohrsche Quantisierungsbedingung: Die Elektronen befinden sich in diskreten stationären Zuständen (auf erlaubten Bahnen), die durch die Bedingung festgelegt sind, dass der Bahndrehimpuls des Elektrons ein ganzzahliges Vielfaches des Planckschen Wirkungsquantums  ist (m_e: Masse des Elektrons):

,

und in denen sich die Elektronen strahlungsfrei bewegen können. Der Bahndrehimpuls des Elektrons im Kernfeld ist also "quantisiert".

b) Bohrsche Frequenzbedingung: Der Übergang von einer erlaubten Bahn der Energie E_n zu einer anderen der Energie E_m erfolgt nicht kontinuierlich, sondern durch einen Quantensprung, wobei die Energiedifferenz zwischen den Zuständen in Form elektromagnetischer Strahlung emittiert bzw. absorbiert wird. Die Beziehung zwischen den Energien der stationären Zustände und den Frequenzen n_nm der Spektrallinien ist dabei gegeben durch

.

c) Bohrsches Korrespondenzprinzip: Für grosse Quantenzahlen n, m geht die Frequenzbedingung in die klassische Umlauffrequenz  des Elektrons um den Kern über (: Umlaufgeschwindigkeit).

Aus der klassischen elektrostatischen Gleichgewichtsbedingung zwischen der abstossenden Zentrifugalkraft und der anziehenden Coulomb-Kraft eines Atomkerns der Kernladungszahl Z

und der Bohrschen Quantisierungsbedingung können die Radien und Energien der erlaubten Bahnen hergeleitet werden:

.

Dabei bedeuten a₀ = 0,529177 × 10 ^{- 10} m den Bohrschen Radius, e die Elementarladung und e₀ die Dielektrizitätskonstante des Vakuums (vgl. Abb.). Die Frequenz n_nm der bei einem Übergang emittierten (n > m bzw. E_n > E_m) oder absorbierten (E_m > E_n) elektromagnetischen Strahlung ergibt sich nach der Bohrschen Frequenzbedingung zu:

.

Unter Anwendung des Korrespondenzprinzips oder durch direkten Vergleich mit der dem Rydberg-Ritzschen Kombinationsprinzip entsprechenden Serienformel kann aus diesem Ergebnis ein Ausdruck für die Rydberg-Konstante hergeleitet werden:

,

der ziemlich gut mit dem aus dem Wasserstoffspektrum bestimmten Wert übereinstimmt. Quantitative Übereinstimmung erhält man, wenn auch die Mitbewegung des Atomkerns (Protons) berücksichtigt wird.

Die Bohrsche Theorie beschreibt die Grobstruktur der Spektren des Wasserstoffatoms sowie der wasserstoffähnlichen Atome sehr gut und konnte einige bemerkenswerte Erfolge verzeichnen. Ausser der Herleitung der Balmer-Formel und der Rydberg-Konstante gehören dazu die Identifikation der Pickering-Serie als Spektrum des He ⁺ -Ions sowie die Interpretation des Stark-Effekts, des Moseleysche Gesetzes und des Franck-Hertz-Versuchs.

Schliesslich konnte Sommerfeld 1915/16 auch die im Spektrum des Wasserstoffs beobachtete Feinstruktur beschreiben, indem er sowohl die aus der Speziellen Relativitätstheorie folgende Geschwindigkeitsabhängigkeit der Elektronenmasse als auch elliptische Bahnen als mögliche stationäre Zustände der Elektronen in die Bohrsche Theorie integrierte (Bohr-Sommerfeldsche Theorie). Dafür verallgemeinerte er die Bohrsche Quantisierungsbedingung zu der Forderung, dass das Phasenintegral über zwei kanonisch konjugierte Variable p, q ein ganzzahliges Vielfaches von h sein sollte (Bohr-Sommerfeldsche oder Wilson-Sommerfeldsche Quantisierungsbedingung):

.

Diese Quantisierungsbedingung kann im Rahmen der Quantenmechanik mit Hilfe der WKB-Näherung deduziert werden. Die Charakterisierung der stationären Zustände erfolgt dann durch zwei Quantenzahlen, von denen die Hauptquantenzahl n die grosse Halbachse der Ellipse und die Nebenquantenzahl k = 1, . . . , n die kleine Halbachse bestimmt, so dass sich für n = k die Bohrschen Kreisbahnen ergeben. Da die Bahngeschwindigkeit für die elliptischen Bahnen nicht mehr konstant und etwas verschieden von der für Kreisbahnen ist, führt die Berücksichtigung der relativistischen Kinematik zu einer kleinen Aufspaltung der Energien zu Bahnen mit verschiedenem k, deren berechnete Werte sehr gut die beobachtete Feinstruktur des Wasserstoffspektrums wiedergeben. Die Anwendung der Bohr-Sommerfeldschen Theorie auf Atome mit mehreren Elektronen lieferte allerdings nur für die Alkaliatome, die in guter Näherung als Einelektronenatome aufgefasst werden können, vergleichbar gute Ergebnisse. Dagegen liessen sich auf dieser Basis weder andere Atome mit mehreren Elektronen noch die chemische Bindung und die Molekülspektren verstehen. Hinzu kommt, dass die Bohrsche Theorie auch die Stabilität der Atome in Form der Modellannahme für die Existenz stationärer Zustände lediglich ad hoc postuliert, aber nicht in dem Sinn erklärt, dass die Stabilität aus der Theorie deduzierbar ist.

Aus heutiger Sicht nimmt die Bohrsche Theorie in dem Sinne ein Zwischenstadium zwischen klassischer Physik und Quantenmechanik ein, als sie von beiden gewisse Resultate übernimmt bzw. vorwegnimmt, letztlich aber mit beiden im Widerspruch steht: Einerseits widerspricht die Vorstellung strahlungsfreier Elektronenbahnen der klassischen Elektrodynamik, andererseits zeigen sich auch an verschiedenen Stellen Inkonsistenzen zur Quantenmechanik, von denen zwei als exemplarisch gelten können:

1) Gemäss der Bohrschen Quantisierungsbedingung ist der Bahndrehimpuls zwar quantisiert, im Unterschied zur Quantenmechanik wird er aber durch die Hauptquantenzahl n und nicht durch die Bahndrehimpulsquantenzahl l bestimmt; insbesondere verschwindet der Bahndrehimpuls des Elektrons im Grundzustand des Wasserstoffatoms in der quantenmechanischen Betrachtung.

2) Im Widerspruch sowohl zu den Lösungen der Schrödinger-Gleichung als auch zur experimentellen Erfahrung steht die Tatsache, dass die Bohrsche Theorie ebene Bahnen der Elektronen im Zentralfeld des Kerns vorhersagt.

Der tiefere Grund für diese Inkonsistenzen ist das Festhalten der Bohrschen Theorie am klassischen Bahnbegriff für die Beschreibung der Elektronenbewegung, den die Quantenmechanik verwirft. Aufgrund dieser Inkonsistenzen kann es weder einen stetigen Übergang von der Bohrschen Theorie zur Quantenmechanik geben, wie man ihn beispielsweise mit gewissen Einschränkungen von der Newtonschen Mechanik zur Speziellen Relativitätstheorie konstruieren kann (abgeschlossene Theorie), noch kann die Bohrsche Theorie als Spezialtheorie für Einelektronensysteme in die Quantenmechanik integriert werden.

Ihre überragende Bedeutung liegt vielmehr darin, dass sie am Beginn eines Umdenkens in der Physik steht, das die Entwicklung in diesem Jahrhundert entscheidend geprägt hat. Die wichtigsten Erkenntnisse der Bohrschen Theorie - das sind insbesondere die Möglichkeit unstetiger, also sprunghafter Änderungen physikalischer Grössen, die Existenz stationärer Elektronenzustände im Atom und die Zuordnung der Spektrallinien zu den Übergängen zwischen diesen stationären Zuständen - sind als Grundprinzipien für die Interpretation sämtlicher spektroskopischer Methoden der Atom-, Molekül- und Festkörperphysik zentraler Bestandteil der modernen Physik geworden. [MG1]

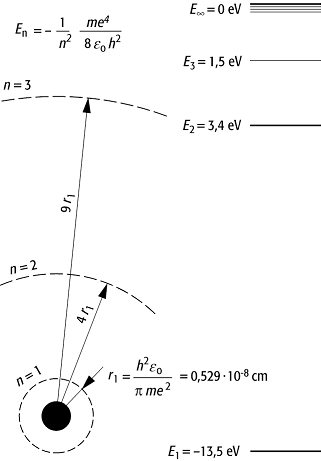
Bohrsche Theorie: Bahnradien und Energieniveaus.