Techniklexikon

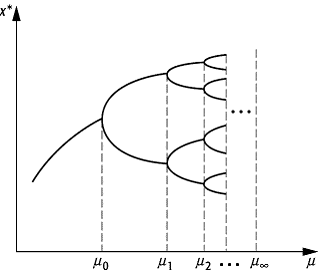
Feigenbaum-Szenario

Nichtlineare Dynamik, Chaos, Fraktale, Periodenverdopplungs-Szenario, Periodenverdopplungs-Route zum Chaos, neben dem Pomeau-Manneville-Szenario und dem Ruelle-Takens-Newhouse-Szenario einer der wichtigsten universellen Wege zu chaotischem Verhalten (Routen ins Chaos, deterministisches Chaos), der durch Veränderung eines Kontrollparameters herbeigeführt werden kann. Das Phänomen des Übergangs zum Chaos durch eine unendliche Reihe von Periodenverdopplungen wurde zunächst für die logistische Abbildung x_t+1 = mx_t(1 - x_t) gefunden und, nachdem M.J. Feigenbaum dessen Universalität erkannt hatte, in vielen Experimenten, wie z.B. dem Rayleigh-Benard-Experiment oder dem Couette-Taylor-Experiment, gemessen. Die Sequenz von Periodenverdopplungen (Feigenbaum-Sequenz), die man bei Variation eines Kontrollparameters m erhält und die dieses Szenario charakterisiert, ist in der Abb. für eine iterierte Abbildung x_t+1 = f_m(x_t) mit einem quadratischen Maximum und negativer Schwarzscher Ableitung  schematisch dargestellt: Für m < m₀ ist ein Fixpunkt stabil (durchgezogene Linie), der bei m₀ instabil wird (gestrichelt) und in einen stabilen Orbit der Periode 2 bifurkiert: . Dieser Orbit, der aus den stabilen Fixpunkten der zweiten Iterierten  besteht, wird bei m₁ > m₀ wiederum instabil und führt über Periodenverdopplung zu einem stabilen Periode-4-Zyklus im Parameterbereich m₁ < m < m₂, dann zur Periode 8 usw. Da Periodenverdopplung einer Halbierung der jeweiligen Grundfrequenz entspricht, spricht man auch von einer Sequenz subharmonischer Bifurkationen. Die sukzessive Halbierung der Grundfrequenz wird experimentell meist durch Messung des Leistungsspektrums erfasst. Generell existiert in dem resultierenden Bifurkationsdiagramm (»Feigenbaum«) im Intervall m_n-1 < m < m_n ein stabiler Orbit der Periode 2ⁿ, der aus den stabilen Fixpunkten der 2ⁿ-ten Iterierten  besteht. Die Bifurkations-Parameter m_n häufen sich entsprechend einer geometrischen Progression an einem Punkt , wobei das Verhältnis  die universelle Feigenbaum-Konstante darstellt. Bei m_¥ ist der Attraktor nicht mehr periodisch, sondern ein Fraktal (Feigenbaum-Attraktor) mit fraktaler Dimension D = 0,5388... Es existiert noch eine weitere universelle Feigenbaum-Konstante a = 2,502807..., die die Skalierung der »Gabel-Öffnungen« in der Nähe des Funktionsmaximums beschreibt. Die Universalität der Konstanten und des Skalenverhaltens folgt aus der Tatsache, dass  und die Funktion  nach Skalierung mit a für grosse n in der Nähe des Maximums von f(x) immer ähnlicher werden: , so dass schliesslich in die Bestimmung von a nur noch die Ordnung des Maximums und die Dimensionalität der Abbildung eingeht. Die angegebenen Werte für a und d gelten für alle eindimensionalen Abbildungen mit quadratischem Maximum. Für Periodenverdopplungs-Szenarien mit anderer Ordnung des Maximums oder z.B. in zweidimensionalen flächenerhaltendenden Abbildungen gelten ähnliche Skalenargumente, die aber auf andere universelle Werte für a und d führen. [GR2]

Feigenbaum-Szenario: Bifurkationsdiagramm für eine iterierte Abbildung x_t+1 = f_m(x_t). Für m < m₀ ist ein Fixpunkt stabil (durchgezogene Linie), der bei m₀ instabil wird (gestrichelt) und in einen stabilen Orbit der Periode 2 bifurkiert. Dieser Orbit, der aus den stabilen Fixpunkten der zweiten Iterierten besteht, wird bei m₁ > m₀ instabil, usw.