Techniklexikon

Maxwell-Gleichungen

Elektrodynamik und Elektrotechnik, die Grundgleichungen der klassischen Elektrodynamik, die alle Erscheinungen des Elektromagnetismus und der Optik beinhalten. Die Gleichungen sind partielle, lineare, gekoppelte Differentialgleichungen erster Ordnung; sie wurden in den Jahren 1861-64 von J.C. Maxwell im Rahmen seiner »dynamischen Theorie des elektromagnetischen Feldes« aufgestellt. Diese baut wesentlich auf dem Feldbegriff M. Faradays auf, der den Elektromagnetismus als Nahwirkungstheorie formulierte.

Die Maxwell-Gleichungen lauten

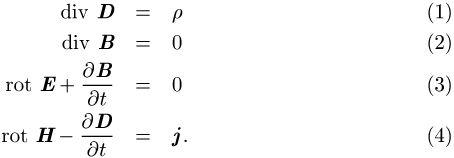
Dabei beschreiben die Feldgrössen E (elektrische Feldstärke), D (dielektrische Verschiebung), B (magnetische Flussdichte) und H (magnetische Feldstärke) die elektrischen und magnetischen Felder. Zwischen ihnen vermitteln die Materialgleichungen E = eD bzw. B = mH. r ist die elektrischen Ladungsdichte, j die Stromdichte, in stromleitenden Medien gilt das erweiterte Ohmsche Gesetz j = sE (s: elektrische Leitfähigkeit). Der Term  wird auch Maxwellscher Verschiebungsstrom genannt; er wurde von Maxwell eingeführt, um das Gleichungsystem widerspruchsfrei zu machen, und führt dazu, dass allein die Änderung eines elektrischen Feldes (z.B. beim Be- und Entladen eines Kondensators) ein Magnetfeld hervorruft.

Der physikalische Inhalt der Gleichungen besagt folgendes:(1): Die elektrischen Ladungen stellen Quellen und Senken des elektrischen Feldes dar.(2): Das magnetische Feld ist quellfrei, es gibt keine isolierten magnetischen Monopole.(3): Zeitliche Änderungen des magnetischen Flusses erzeugen Wirbel im elektrischen Feld (Faradaysches Induktionsgesetz).(4): Leitungs- und Verschiebungsströme erzeugen Wirbel im magnetischen Feld, sie werden oft auch (etwas unexakt) als Quellen des Magnetfeldes bezeichnet (Ampèresche Gesetze).

Im Vakuum (r = 0, j = 0, e = e₀, m = m₀) vereinfachen sich die Maxwell-Gleichungen zu div E = div B = 0, rot E = -¶B / ¶t und rot B / m₀ = e₀¶E / ¶t. Hieraus folgen unmittelbar die Wellengleichungen im Vakuum

und somit die Existenz elektromagnetischer Wellen.

Die Tatsache, dass die Maxwell-Gleichungen nicht invariant unter Galilei-Transformationen sind, führte zur Entdeckung der Speziellen Relativitätstheorie. Die relavistische Invarianz sieht man am einfachsten in der kovarianten Formulierung der Elektrodynamik,

mit

wobei  und ; aus den Potentialen A⁰ und A lassen sich die Felder ableiten,