Techniklexikon

Potential

Klassische Mechanik, im weiteren Sinn eine von bestimmten physikalischen Grössen (z.B. Ortskoordinate) abhängende Funktion, aus der sich durch partielle Differentiation nach diesen andere physikalische Grössen (z.B. Feldstärke) bestimmen lassen. 1) Der Begriff entstammt der Mechanik, in der das Potential eine skalare Ortsfunktion U(r) ist, aus der man durch Differentiation die Kraft F, die an einem gegebenen Ort r auf eine Probemasse wirkt, erhält: . Der Gradientenoperator ist dabei definiert als

wobei  die Einheitsvektoren in Richtung der Koordinatenachsen darstellen. Die Richtung der Kraft F ist senkrecht zu den Äquipotentiallinien (bzw. -flächen), die gleiche Werte der Potentialfunktion aufweisen (siehe Abb.).

Das Potential wird über den Begriff der Arbeit eingeführt: längs des Weges von r₁ nach r₂ verrichtet die Kraft F die Arbeit

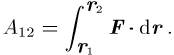
Wenn A₁₂ von der Wegführung unabhängig ist, folgt daraus, dass jedem Punkt r eine eindeutige Funktion U(r), das Potential, zugeordnet werden kann. Die Differenz U(r₁) - U(r₂) ist dann proportional zur Arbeit A₁₂, die Proportionalitätskonstante ist die Masse m: . Die physikalische Observable in dieser Gleichung ist die Arbeit, die durch Differenzenbildung erhalten wird. Es ändert sich also nichts, wenn zu allen Potentialwerten eine willkürliche, skalare Konstante addiert wird: . Diese Konstante wird im allgemeinen so festgelegt, dass das Portential im Unendlichen verschwindet: . In der Mechanik wird gelegentlich die Konvention verwendet, die Masse des Probekörpers in die Definition des Potentials mit einzubeziehen, richtigerweise sollte man bei der Funktion  von der potentiellen Energie sprechen, um eine einheitliche Definition des Potentialbegriffs in Mechanik und Elektrodynamik zu erhalten. Aus der Definition des Potentials folgt, dass eine Kraft in einem Potentialfeld längs einer geschlossenen Kurve S bei der Rückkehr zum Ausgangspunkt keine Arbeit verrichtet:

Das Wegintegral längs der geschlossenen Kurve kann nach dem Stokesschen Integralsatz umgewandelt werden in

Die Integrationsfläche A wird von der Kurve S berandet. Das Verschwinden der Vektoroperation Rotation  für Kräfte, die aus einem Potential abgeleitet werden können, bedeutet, dass das Feld F keine Wirbel aufweist, d.h. keine geschlossenen Kraftlinien besitzt, die bei der Integration  einen Beitrag leisten würden.

Die eingeführten Konzepte sollen am Beispiel des Gravitationsfeldes einer Punktmasse M klar gemacht werden. Gemäss dem Newtonschen Gravitationsgesetz ist in diesem Feld die Kraft auf eine Probemasse m im Abstand r . Man kann durch Rechnung zeigen, dass die Gravitationskraft der Bedingung  genügt und aus einem Potential abgeleitet werden kann. Um die Potentialfunktion zu konstruieren, beginnt man mit der Arbeit längs einer infinitesimalen Wegstrecke dr. Um die Probemasse m unendlich weit von M wegzutransportieren, ist die Arbeit

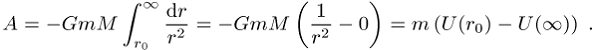
Es folgt für die Potentialfunktion des Gravitationsfeldes der Masse M: , wobei von der Konvention  Gebrauch gemacht wurde.

2) Elastizitätslehre: elastische Energiedichte.

3) Elektrostatik, Elektrodynamik: elektrisches Potential.

4) Physikalische Chemie: elektrochemisches Potential.

5) Thermodynamik: chemisches Potential, thermodynamische Potentiale.

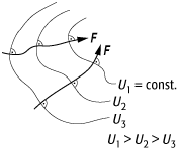
Potential: Die Kraft F steht jeweils senkrecht auf den Äquipotentiallinien U_i.