Abbildungsgleichungen

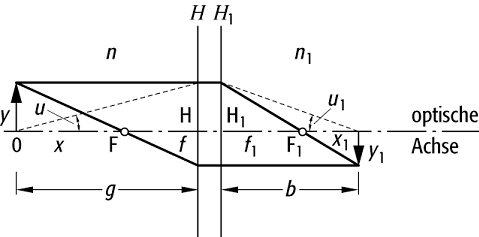
bei der geometrisch-optischen Abbildung für das paraxiale Gebiet geltende Beziehungen zwischen konjugierten Grössen in Objekt- und Bildraum (Objektweite, Bildweite, Massstäbe der Abbildungen, usw.). Das abbildende System wird hierbei durch seine Hauptpunkte (Kardinalelemente) H und H₁ als Bezugspunkte der Bestimmung der Brennweiten sowie der Objekt- und Bildweiten ersetzt. Zur eindeutigen Angabe von Lage und Grösse von Objekt und Bild wird konventionell die Lichtrichtung von links nach rechts angenommen, und die Strecken bezüglich der Lichtrichtung bzw. optischen Achse werden durch entsprechende Vorzeichen gekennzeichnet.

Die Grundgleichung für ein achsensymmetrisches Strahlenbündel und für Strecken parallel zur optischen Achse (axiale Strecken) lautet:

 (allgemeine Abbildungsgleichung).

Dabei sind f und f₁ die Brennweiten im Objekt- bzw. Bildraum und g und b die Objekt- bzw. Bildweite (Abstände von den Hauptpunkten), siehe Abb. Mit der Einführung von x = g - f, x₁ = b - f₁ (Objekt- bzw. Bildweiten von den Brennpunkten aus gemessen) ergibt sich die Newtonsche Form der Abbildungsgleichung:

,

mit der man sofort zur sog. Axialvergrösserung (Tiefenvergrösserung) a gelangt:

.

Für senkrecht auf der optischen Achse stehende Strecken (laterale Strecken) gilt die Abbildungsgleichung

die die Lateralvergrösserung b (den Abbildungsmassstab) beschreibt (n und n₁ sind die Brechzahlen im Objekt- bzw. Bildraum mit n/n₁ = f/f₁, y und y₁ bezeichnen die achsensenkrechten Objekt- bzw. Bildgrössen).

Schliesslich lässt sich noch eine Abbildungsgleichung angeben, über die die Angularvergrösserung definiert ist:

.

Dabei sind u und u₁ Neigungswinkel zweier konjugierter Strahlen im Bild- bzw. Objektraum (Neigung gegen die optische Achse).

Für die Vergrösserungen gilt weiter: . Als Hauptebenen H, und H₁ einer optischen Abbildung bezeichnet man diejenigen konjugierten Ebenen in Objekt- und Bildraum, für die b =  + 1 ist. Gilt g =  + 1, so spricht man von Knotenebenen. Ist die Brechzahl n in Bild- und Objektraum identisch, so fallen Haupt- und Knotenebenen zusammen und haben von den Brennebenen den Abstand x = f und x₁ =  - f, es gilt a =  - b² und die Abbildungsgleichungen für axiale Strecken vereinfachen sich zu:

 und .

Die Abbildungsgleichungen gelten für viele aufeinanderfolgende Abbildungen und streng nur im paraxialen Gebiet.

Abbildungsgleichungen: Der Lichtstrahl gelangt von links in das optische System und bildet entsprechend den Abbildungsgleichungen den Gegenstand ab, weitere Erläuterungen im Text.