Techniklexikon

Finite-Elemente-Methode

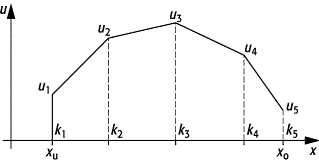
Quantenmechanik, FEM, Methode der finiten Elemente, eine der wichtigsten Näherungsmethoden zur Lösung von Feldproblemen der Naturwissenschaft und Technik. Die FEM ist eine Diskretisierungsmethode, d.h. die Randwertaufgabe wird durch ein lineares Gleichungssystem mit endlich vielen Unbekannten approximiert; dabei will man Näherungswerte nur an endlich vielen Punkten, den Knotenpunkten, des Lösungsintervalls bestimmen. In der Regel nimmt man an, dass die Funktionen sich in diesen Gebieten als Polynom darstellen lassen, die in den Knotenpunkten die Näherungswerte der Lösung des Randwertproblems annehmen. Die Teilintervalle, in denen oft ein linearer Verlauf vorausgesetzt wird (Abb. 1), heissen finite Elemente. Das Funktionsverhalten zwischen den zwei Knotenpunkten kann man durch lineare Interpolation ermitteln:

,

Die rechentechnische Realisierung dieser Interpolation ist leicht möglich. Zur Bestimmung der FEM-Näherung für die Lösung des Randwertproblems

(G^(D) und G^(N) disjunkt bezüglich G = {x_u, x_o}) ist es notwendig, die Zahlenwerte der stückweise linearen Funktion zu bestimmen. Dazu benutzt man die Variationsgleichung

 (Abb.2), für die bestimmte Vergleichsfunktionen im Verlauf vorgegeben sind. Das entstehende Gleichungssystem wird mit Hilfe des Ritz-Galerkin-Verfahrens gelöst.

Finite-Elmente-Methode 1: Stückweise lineare Funktion.

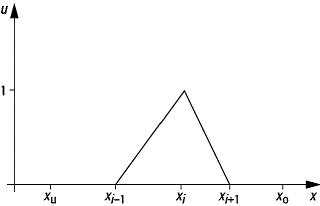
Finite-Elemente-Methode 2: Vergleichsfunktion der linearen FEM.