Kurven und Flächen im Raum

Petra Nordinghaus-Martin
spezielle Abbildungen
von ![]() und
und ![]() in den Vektorraum
in den Vektorraum ![]() , die
insbesondere in der Differentialgeometrie untersucht werden. In der Mechanik
wird manchmal die Bewegung von Teilchen entlang von Raumkurven oder auf Flächen
untersucht. Raumkurven werden gewöhnlich durch
, die
insbesondere in der Differentialgeometrie untersucht werden. In der Mechanik
wird manchmal die Bewegung von Teilchen entlang von Raumkurven oder auf Flächen
untersucht. Raumkurven werden gewöhnlich durch
![]()
parametrisiert. Die Bogenlänge s zwischen zwei Raumpunkten r1 und r2 folgt aus
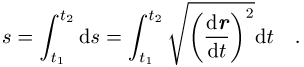
Bei gegebenem Fusspunkt r1 stellt die Bogenlänge s eine besonders nützliche Parametrisierung von Raumkurven dar. Der Einheitsvektor
![]()
gibt die Richtung der Tangente im Punkt r(t); er zeigt in die positive Kurvenrichtung. Mit Hilfe der zweiten Ableitung
![]()
kann die Krümmung k und der Hauptnormalenvektor n berechnet werden; r = 1 / k
heisst Krümmungsradius. t und n spannen zusammen die Schmiegungsebene einer Raumkurve
in einem bestimmten Punkt auf. Aus den zueinander orthogonalen Vektoren t und n lässt sich mit der
Binormalen ![]() das begleitende Dreibein
das begleitende Dreibein ![]() bilden; die von t
und b aufgespannte Ebene heisst auch
rektifizierende Ebene. Schliesslich lässt sich noch die Windung bzw. Torsion w einer Raumkurve definieren:
bilden; die von t
und b aufgespannte Ebene heisst auch
rektifizierende Ebene. Schliesslich lässt sich noch die Windung bzw. Torsion w einer Raumkurve definieren:
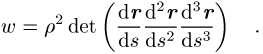
Ist ![]() in allen Kurvenpunkten, so liegt die Raumkurve
in einer Ebene. Ist die Raumkurve nicht nach s
parametrisiert, so gilt
in allen Kurvenpunkten, so liegt die Raumkurve
in einer Ebene. Ist die Raumkurve nicht nach s
parametrisiert, so gilt
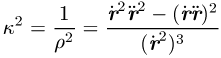
und 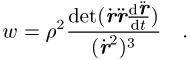
Damit lassen sich nun die Fresnelschen Formeln, die Beziehungen zwischen den Ableitungen der Vektoren t, n, b des begleitenden Dreibeins beschreiben, beweisen:
![]()
![]()
![]()
Flächen im Raum bieten in Verallgemeinerung von (*) die
Möglichkeit der Parametrisierung ![]() . Daneben
können Flächen im Raum explizit, d.h.
. Daneben
können Flächen im Raum explizit, d.h. ![]() , oder
implizit durch
, oder
implizit durch ![]() definiert werden. Als Beispiel sei mit
definiert werden. Als Beispiel sei mit ![]() die Oberfläche einer Kugel mit Radius R genannt:
die Oberfläche einer Kugel mit Radius R genannt:
![]()
![]()
![]()
Die implizite Darstellung lautet ![]() . Die
Tangentenvektoren einer Fläche in einem Punkt der Fläche sind
. Die
Tangentenvektoren einer Fläche in einem Punkt der Fläche sind
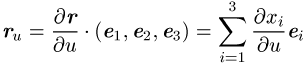
und 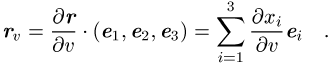
Mit Hilfe der Tangentialvektoren lässt sich wieder der
Normalenvektor 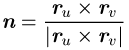
konstruieren, aber auch das Flächenelement ![]() berechnen.
berechnen.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.