lineare Unabhängigkeit

Julian Schultheiss
die Eigenschaft einer endlichen Menge von
Vektoren ![]() eines Vektorraums V
über den Körper K, dass diese den Nullvektor nur in
trivialer Weise erzeugen können, d.h.
eines Vektorraums V
über den Körper K, dass diese den Nullvektor nur in
trivialer Weise erzeugen können, d.h.
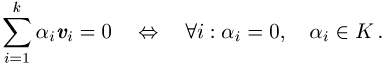
Beispiele für Systeme linear unabhängiger Vektoren sind die
Einheitsvektoren ![]() des
des ![]() oder die Monome
oder die Monome ![]() . Liegt ein
Vektor
. Liegt ein
Vektor ![]() in dem von
in dem von ![]() aufgespannten Untervektorraum, so kann
aufgespannten Untervektorraum, so kann ![]() eindeutig aus den Vektoren
eindeutig aus den Vektoren ![]() kombiniert werden. Ist
kombiniert werden. Ist ![]() ein System n
linear unabhängiger Vektoren eines n-dimensionalen
Vektorraums V, so ist
ein System n
linear unabhängiger Vektoren eines n-dimensionalen
Vektorraums V, so ist ![]() eine Basis des Vektorraums V.
eine Basis des Vektorraums V.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.