Techniklexikon

Vektor

Mathematische Methoden und Computereinsatz, Element eines Vektorraums. Ob ein Objekt als Vektor angesehen werden kann, entscheidet sich durch die Rechenregeln, denen es genügt; Vektoren genügen den Vektorraumaxiomen (Vektorraum). Beispiel: das -Tupel  bildet einen Vektor  des -dimensionalen Vektorraums . Viele Grössen in der Physik, z.B. die Geschwindigkeit , die Beschleunigung , die Kraft , der Drehimpuls  oder die elektrische Feldstärke , lassen sich durch Vektoren darstellen; hierbei ist wichtig, dass diesen Vektoren eine Richtung und ein Betrag zugewiesen ist. In der Physik wird ein Vektor auch häufig durch sein Transformationsverhalten charakterisiert; im Gegensatz zu echten Vektoren gibt es in diesem Kontext noch Pseudovektoren.

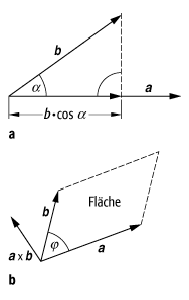
Vektor 1: a) Skalarprodukt a × b = a b cosa zweier Vektoren. b) Vektorprodukt (Kreuprodukt) zweier Vektoren a und b, definiert als ein auf a und b senkrecht stehender Vektor, dessen Betrag dem Flächeninhalt des von a und b aufgespannten Parallelogramms entspricht: |a ´ b| = |a| |b| sin j.

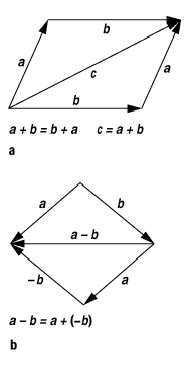
Vektor 2: a) Vektoraddition: a + b = b + a, c = a + b. b) Vektorsubtraktion: a - b = a + (-b).