Stringtheorie

Hermann Loring
Teilchenphysik
1 Anfänge
Die Anfänge der
Stringtheorie gehen auf den Versuch zurück, Ordnung in die Vielzahl der
experimentell gemessenen hadronischen Resonanzzustände, ihre
Massen-Drehimpuls-Relationen sowie das Hochenergieverhalten hadronischer
Streuamplituden zu bringen. Einen Meilenstein dieser Entwicklungen stellt die
1968 postulierte Veneziano-Amplitude dar, die die empirisch motivierte Dualitätshypothese
realisiert. Diese besagt, dass sich die vollständigen Streuamplituden auf zwei
duale Weisen berechnen lassen: entweder durch Summation über alle ![]() -Kanal- oder
alternativ alle
-Kanal- oder
alternativ alle ![]() -Kanal-Feynman-Diagramme
(Mandelstam-Variablen). Die Veneziano-Amplitude kann als Streuamplitude einer
Theorie eindimensionaler Objekte, sogenannter Strings, hergeleitet werden. Die
hadronischen Zustände sind die harmonischen Anregungen des Strings, und ihre
Massen ergeben sich als ganzzahlige Vielfache einer charakteristischen
Energieskala, die durch die Stringspannung
-Kanal-Feynman-Diagramme
(Mandelstam-Variablen). Die Veneziano-Amplitude kann als Streuamplitude einer
Theorie eindimensionaler Objekte, sogenannter Strings, hergeleitet werden. Die
hadronischen Zustände sind die harmonischen Anregungen des Strings, und ihre
Massen ergeben sich als ganzzahlige Vielfache einer charakteristischen
Energieskala, die durch die Stringspannung ![]() gesetzt wird. Alle Zustände liegen auf
parallelen Regge-Trajektorien mit Drehimplus
gesetzt wird. Alle Zustände liegen auf
parallelen Regge-Trajektorien mit Drehimplus ![]() und Steigung
und Steigung ![]() . Die Grösse
. Die Grösse ![]() ist die für die Stringtheorie
charakteristische Längenskala.
ist die für die Stringtheorie
charakteristische Längenskala.
Diskrepanzen mit tiefinelastischen Streuexperimenten, insbesondere dem Partonverhalten von Hadronen (Partonmodell), beendeten den Versuch, die Stringtheorie als eine Theorie der starken Wechselwirkung zu verfolgen. Nach dem Beweis der Renormierbarkeit nicht-abelscher Eichtheorien fand die starke Wechselwirkung ihre adäquate Beschreibung in der Quantenchromodynamik.
Heute wird die
Stringtheorie als Kandidat für eine Theorie der Quantengravitation mit ![]() (Planck-Länge) diskutiert. Ausschlaggebend
dafür ist die Tatsache, dass die Stringtheorie immer genau eine masselose
Anregung mit Spin 2 besitzt. Auf Grund seiner Streuamplituden wird diese
Anregung mit dem Graviton, dem Austauschteilchen der
Gravitationswechselwirkung, identifiziert. Damit ist diese notwendigerweise
Bestandteil der Stringtheorie und die Newtonsche Gravitationskonstante mit der
Stringspannung verknüpft. Darüberhinaus können nicht nur das Graviton, sondern
alle heute bekannten Elementarteilchen als (masselose) Anregungsmoden des
Strings auftreten. Das ermöglicht eine Vereinheitlichung aller
Elementarteilchen und ihrer Wechselwirkungen im Rahmen der Stringtheorie.
(Planck-Länge) diskutiert. Ausschlaggebend
dafür ist die Tatsache, dass die Stringtheorie immer genau eine masselose
Anregung mit Spin 2 besitzt. Auf Grund seiner Streuamplituden wird diese
Anregung mit dem Graviton, dem Austauschteilchen der
Gravitationswechselwirkung, identifiziert. Damit ist diese notwendigerweise
Bestandteil der Stringtheorie und die Newtonsche Gravitationskonstante mit der
Stringspannung verknüpft. Darüberhinaus können nicht nur das Graviton, sondern
alle heute bekannten Elementarteilchen als (masselose) Anregungsmoden des
Strings auftreten. Das ermöglicht eine Vereinheitlichung aller
Elementarteilchen und ihrer Wechselwirkungen im Rahmen der Stringtheorie.
2 Der freie String
Die Dynamik des
bosonischen Strings im ![]() -dimensionalen
Minkowski-Raum wird durch die Nambu-Goto-Wirkung
-dimensionalen
Minkowski-Raum wird durch die Nambu-Goto-Wirkung
![]()
beschrieben. Das
Integral ist der Flächeninhalt der durch ![]() parametrisierten, vom String überstrichenen
Weltfläche
parametrisierten, vom String überstrichenen
Weltfläche ![]() in der auf ihr induzierten Metrik
in der auf ihr induzierten Metrik ![]() .
. ![]() beschreibt die Einbettung der Weltfläche in
die
beschreibt die Einbettung der Weltfläche in
die ![]() -dimensionale
Raumzeit
-dimensionale
Raumzeit ![]() mit Minkowski-Metrik
mit Minkowski-Metrik ![]() ,
, ![]() .
. ![]() ist die direkte Verallgemeinerung der Wirkung
punktförmiger (nulldimensionaler) relativistischer Teilchen auf eindimensionale
Strings. Die Weltfläche eines frei propagierenden offenen Strings hat die
Topologie eines Streifens und die eines geschlossenen Strings die eines
Zylinders; im geschlossenen String ist
ist die direkte Verallgemeinerung der Wirkung
punktförmiger (nulldimensionaler) relativistischer Teilchen auf eindimensionale
Strings. Die Weltfläche eines frei propagierenden offenen Strings hat die
Topologie eines Streifens und die eines geschlossenen Strings die eines
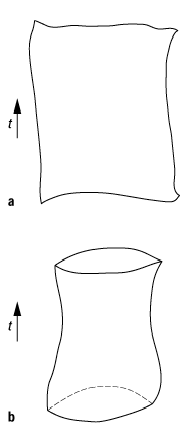
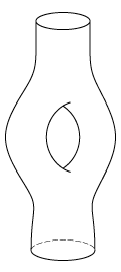
Zylinders; im geschlossenen String ist ![]() periodisch auf dem Zylinder (siehe [37]Abb. 1).
periodisch auf dem Zylinder (siehe [37]Abb. 1).
Im offenen String kann
man entweder Dirichletsche (D) oder Neumannsche (N) Randbedingungen an jedes
der ![]() Felder
Felder ![]() an jedem der beiden Ränder der Weltfläche
stellen. Physikalisch bedeuten Neumannsche Randbedingungen, dass kein
Raumzeit-Impuls über das Ende des Strings abfliesst; bei Dirichletschen
Randbedingungen fliesst dagegen Impuls ab. Die
an jedem der beiden Ränder der Weltfläche
stellen. Physikalisch bedeuten Neumannsche Randbedingungen, dass kein
Raumzeit-Impuls über das Ende des Strings abfliesst; bei Dirichletschen
Randbedingungen fliesst dagegen Impuls ab. Die ![]() -dimensionale
Poincaré-Invarianz (Poincaré-Gruppe) der Theorie verlangt, dass dieser Impuls
auf andere dynamische Objekte übertragen wird. Diese Objekte, auf denen offene
Strings enden, heissen Dirichlet-Branes oder D-Branes (»Brane« ist eine
Erweiterung von engl. »Membrane«). Haben
-dimensionale
Poincaré-Invarianz (Poincaré-Gruppe) der Theorie verlangt, dass dieser Impuls
auf andere dynamische Objekte übertragen wird. Diese Objekte, auf denen offene
Strings enden, heissen Dirichlet-Branes oder D-Branes (»Brane« ist eine
Erweiterung von engl. »Membrane«). Haben ![]() der räumlichen Komponenten von
der räumlichen Komponenten von ![]() an einem Ende des offenen Strings Neumannsche
Randbedingungen und die übrigen
an einem Ende des offenen Strings Neumannsche
Randbedingungen und die übrigen ![]() Komponenten Dirichletsche Randbedingungen, so
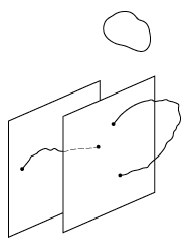
endet dieser String auf einer Dp-Brane. Eine
D0-Brane nennt man auch D-Teilchen und eine D1-Brane einen D-String, der vom
fundamentalen String (F-String) zu unterscheiden ist (siehe [38]Abb. 2).
Komponenten Dirichletsche Randbedingungen, so
endet dieser String auf einer Dp-Brane. Eine
D0-Brane nennt man auch D-Teilchen und eine D1-Brane einen D-String, der vom
fundamentalen String (F-String) zu unterscheiden ist (siehe [38]Abb. 2).
Die Teilchen, die den
Anregungen des offenen Strings entsprechen, propagieren nur auf dem Weltvolumen
der D-Brane, die des geschlossenen Strings dagegen in der ganzen ![]() -dimensionalen
Raumzeit.
-dimensionalen
Raumzeit.
Die Quantisierung der Theorie vereinfacht sich durch die Benutzung der zur Nambu-Goto-Wirkung klassisch äquivalenten Poljakow-Wirkung
![]()
![]() ist die Wirkung von
ist die Wirkung von ![]() Skalarfeldern
Skalarfeldern ![]() , gekoppelt an
die zweidimensionale Gravitation mit Metrik
, gekoppelt an
die zweidimensionale Gravitation mit Metrik ![]() .
. ![]() ist invariant unter globalen
Poincaré-Transformationen der Raumzeit
ist invariant unter globalen
Poincaré-Transformationen der Raumzeit ![]() , unter lokalen
Reparametrisierungen der Weltfläche
, unter lokalen
Reparametrisierungen der Weltfläche ![]() und unter lokalen Weyl-Reskalierungen der
Metrik
und unter lokalen Weyl-Reskalierungen der
Metrik ![]() . Die lokale
Weyl-Invarianz impliziert, dass der Energie-Impuls-Tensor
. Die lokale
Weyl-Invarianz impliziert, dass der Energie-Impuls-Tensor ![]() der Feldtheorie auf der Weltfläche spurfrei
ist:
der Feldtheorie auf der Weltfläche spurfrei
ist: ![]() . Die
Reparametrisierungen erlauben den Übergang zur konformen Eichung
. Die
Reparametrisierungen erlauben den Übergang zur konformen Eichung ![]() (konforme Feldtheorie). Klassisch entkoppelt
auch der Weyl-Freiheitsgrad
(konforme Feldtheorie). Klassisch entkoppelt
auch der Weyl-Freiheitsgrad ![]() . Die
Verletzung der lokalen Weyl-Invarianz in der quantisierten Theorie signalisiert
eine konforme Anomalie.
. Die
Verletzung der lokalen Weyl-Invarianz in der quantisierten Theorie signalisiert
eine konforme Anomalie.
In der
(1,1)-supersymmetrischen Version der Poljakow-Wirkung (Supersymmetrie) wird
jedes bosonische Feld ![]() zusammen mit zwei Majorana-Weyl-Superpartnern
zusammen mit zwei Majorana-Weyl-Superpartnern ![]() positiver bzw. negativer Chiralität an
zweidimensionale Supergravitation
positiver bzw. negativer Chiralität an
zweidimensionale Supergravitation ![]() gekoppelt. Wegen der zweidimensionalen lokalen
Supersymmetrie sind in der klassischen Theorie neben den metrischen
Freiheitsgraden auch diejenigen der Gravitinos
gekoppelt. Wegen der zweidimensionalen lokalen
Supersymmetrie sind in der klassischen Theorie neben den metrischen
Freiheitsgraden auch diejenigen der Gravitinos ![]() unphysikalisch.
unphysikalisch.
Die Fermionen ![]() auf der Weltfläche des geschlossenen Strings
können periodisch (Ramond) oder antiperiodisch (Neveu-Schwarz) sein, wobei die
Periodizitätsbedingungen für die beiden Chiralitäten unabhängig gewählt werden
können. Das führt zu vier verschiedenen »Sektoren« der geschlossenen
Stringtheorie. Im Anregungsspektrum der Stringtheorie sind die Zustände in den
(NS,NS)- und (R,R)-Sektoren Raumzeit-Bosonen, während die Raumzeit-Fermionen
aus den beiden gemischten Sektoren (R,NS) und (NS,R) resultieren. Beim offenen
String koppeln die Randbedingungen die beiden chiralen Weltflächenfermionen,
und man erhält zwei verschiedene Sektoren: den NS-Sektor mit Raumzeit-Bosonen
und den R-Sektor mit Raumzeit-Fermionen.
auf der Weltfläche des geschlossenen Strings
können periodisch (Ramond) oder antiperiodisch (Neveu-Schwarz) sein, wobei die
Periodizitätsbedingungen für die beiden Chiralitäten unabhängig gewählt werden
können. Das führt zu vier verschiedenen »Sektoren« der geschlossenen
Stringtheorie. Im Anregungsspektrum der Stringtheorie sind die Zustände in den
(NS,NS)- und (R,R)-Sektoren Raumzeit-Bosonen, während die Raumzeit-Fermionen
aus den beiden gemischten Sektoren (R,NS) und (NS,R) resultieren. Beim offenen
String koppeln die Randbedingungen die beiden chiralen Weltflächenfermionen,
und man erhält zwei verschiedene Sektoren: den NS-Sektor mit Raumzeit-Bosonen
und den R-Sektor mit Raumzeit-Fermionen.
Die Quantisierung der
Stringtheorie im Minkowski-Raum ist nur in einer kritschen Dimension ![]() möglich, wobei
möglich, wobei ![]() für den bosonischen String und
für den bosonischen String und ![]() für den fermionischen String. Man erhält einen
positiv-definiten Hilbert-Raum (no-ghost-theorem), und sowohl die
Poincaré-Invarianz der Raumzeit wie auch die (Super)Weyl-Invarianz auf der
Weltfläche sind frei von Anomalien. In der kovarianten BRS-Quantisierung führt
die Eichfixierung der lokalen Symmetrien zu Geisterfeldern, den
Reparametrisierungsgeistern
für den fermionischen String. Man erhält einen
positiv-definiten Hilbert-Raum (no-ghost-theorem), und sowohl die
Poincaré-Invarianz der Raumzeit wie auch die (Super)Weyl-Invarianz auf der
Weltfläche sind frei von Anomalien. In der kovarianten BRS-Quantisierung führt
die Eichfixierung der lokalen Symmetrien zu Geisterfeldern, den
Reparametrisierungsgeistern ![]() und ihren Superpartnern
und ihren Superpartnern ![]() . In der
kritischen Dimension wird ihr Beitrag zur konformen Anomalie durch
. In der
kritischen Dimension wird ihr Beitrag zur konformen Anomalie durch ![]() und
und ![]() kompensiert.
kompensiert.
Das resultierende
Spektrum der Stringtheorie enthält eine endliche Anzahl masseloser Anregungen
und unendlich viele massive Anregungen. Dabei treten auch tachyonische Zustände
mit negativem Massequadrat auf. Sie implizieren eine Instabilität des Vakuums.
Dies ist im bosonischen String unvermeidlich. Das Spektrum des fermionischen
Strings muss jedoch durch eine zusätzliche Projektion
(Gliozzi-Scherk-Olive-Projektion (GSO-Projektion)) eingeschränkt werden. Diese
GSO-Projektion kann so gewählt werden, dass u.a. das Tachyon herausprojiziert
wird und gleichzeitig ein Raumzeit-supersymmetrisches Spektrum resultiert. Die
GSO-Projektion ist notwendig und ergibt sich als Konsistenzbedingung (modulare
Invarianz) aus den quantenmechanischen Streuamplituden, die unter Punkt 3 noch
eingehender vorgestellt werden. In einer Theorie mit nur geschlossenen Strings
besitzt das Spektrum zehndimensionale ![]() -Supersymmetrie.
Zwei mögliche, inäquivalente GSO-Projektionen führen zu der nicht-chiralen
Typ-IIA- und der chiralen Typ-IIB-Theorie. Ihr masseloses Spektrum ist das der
zehndimensionalen Typ-IIA- bzw. Typ-IIB-Supergravitationstheorie.
-Supersymmetrie.
Zwei mögliche, inäquivalente GSO-Projektionen führen zu der nicht-chiralen
Typ-IIA- und der chiralen Typ-IIB-Theorie. Ihr masseloses Spektrum ist das der
zehndimensionalen Typ-IIA- bzw. Typ-IIB-Supergravitationstheorie.
Das Spektrum der
Typ-I-Theorie mit offenen und geschlossenen Strings ist ![]() -supersymmetrisch
und enthält im masselosen Sektor eine supersymmetrische Yang-Mills-Theorie
gekoppelt an Supergravitation. Die Freiheitsgrade der Yang-Mills-Theorie liegen
im Anregungsspektrum des offenen Strings. Die beiden Enden des Strings tragen
Ladung in der fundamentalen Darstellung der Eichgruppe (Chan-Paton-Faktoren),
so dass ein offener String die Quantenzahlen eines Eichbosons trägt. Die
Freiheitsgrade der Supergravitation liegen wie in den Typ-II-Theorien im
masselosen Anregungsspektrum des geschlossenen Strings. Die Konsistenz der
Typ-I-Theorie fordert, dass die Eichgruppe die orthogonale Gruppe SO(32) ist
nur dann verschwinden alle Eich- und Gravitationsanomalien.
-supersymmetrisch
und enthält im masselosen Sektor eine supersymmetrische Yang-Mills-Theorie
gekoppelt an Supergravitation. Die Freiheitsgrade der Yang-Mills-Theorie liegen
im Anregungsspektrum des offenen Strings. Die beiden Enden des Strings tragen
Ladung in der fundamentalen Darstellung der Eichgruppe (Chan-Paton-Faktoren),
so dass ein offener String die Quantenzahlen eines Eichbosons trägt. Die
Freiheitsgrade der Supergravitation liegen wie in den Typ-II-Theorien im
masselosen Anregungsspektrum des geschlossenen Strings. Die Konsistenz der
Typ-I-Theorie fordert, dass die Eichgruppe die orthogonale Gruppe SO(32) ist
nur dann verschwinden alle Eich- und Gravitationsanomalien.
Die Typ-I- und
Typ-II-Theorien werden auch als Superstringtheorien bezeichnet. Neben der
Typ-I-Theorie gibt es zwei weitere Stringtheorien mit ![]() -Raumzeit-Supersymmetrie,
den heterotischen E8
´
E8- sowie den
heterotischen SO(32)-String. Diese beiden Stringtheorien haben, wie die
Typ-II-Theorien, nur geschlossene Strings. Im Gegensatz zur
(1,1)-Weltflächensupersymmetrie der Superstringtheorien besitzen die
heterotischen Theorien nur (1,0)-Supersymmetrie. Der Superpartner von
-Raumzeit-Supersymmetrie,
den heterotischen E8
´
E8- sowie den
heterotischen SO(32)-String. Diese beiden Stringtheorien haben, wie die
Typ-II-Theorien, nur geschlossene Strings. Im Gegensatz zur
(1,1)-Weltflächensupersymmetrie der Superstringtheorien besitzen die
heterotischen Theorien nur (1,0)-Supersymmetrie. Der Superpartner von ![]() ist nun ein einziges Majorana-Weyl-Fermion
ist nun ein einziges Majorana-Weyl-Fermion ![]() , und die
Abwesenheit von Gravitationsanomalien auf der Weltfläche erfordert in der
fermionischen Formulierung der Theorie das Hinzufügen von 32 zusätzlichen
Majorana-Weyl-Fermionen
, und die
Abwesenheit von Gravitationsanomalien auf der Weltfläche erfordert in der
fermionischen Formulierung der Theorie das Hinzufügen von 32 zusätzlichen
Majorana-Weyl-Fermionen ![]() . In der
bosonischen Formulierung des heterotischen Strings ersetzt man die 32 Fermionen
durch 16 periodische chirale Skalarfelder
. In der
bosonischen Formulierung des heterotischen Strings ersetzt man die 32 Fermionen
durch 16 periodische chirale Skalarfelder ![]() , die die
Koordinaten eines 16-dimensionalen Torus sind. Modulare Invarianz schränkt die
möglichen Tori auf solche ein, die von einem 16-dimensionalen euklidischen
selbst-dualen geraden Gitter
, die die
Koordinaten eines 16-dimensionalen Torus sind. Modulare Invarianz schränkt die
möglichen Tori auf solche ein, die von einem 16-dimensionalen euklidischen
selbst-dualen geraden Gitter ![]() durch
durch ![]() erzeugt werden. Es gibt genau zwei solche
Gitter, die die beiden Eichgruppen E8 ´ E8 und SO(32) erlauben. Das masselose Spektrum
der heterotischen Stringtheorien ist wiederum eine supersymmetrische
Yang-Mills-Theorie gekoppelt an Supergravitation diesmal mit Eichgruppe E8 ´ E8 oder SO(32).
erzeugt werden. Es gibt genau zwei solche
Gitter, die die beiden Eichgruppen E8 ´ E8 und SO(32) erlauben. Das masselose Spektrum
der heterotischen Stringtheorien ist wiederum eine supersymmetrische
Yang-Mills-Theorie gekoppelt an Supergravitation diesmal mit Eichgruppe E8 ´ E8 oder SO(32).
3 Wechselwirkende Strings
Die bisherige
Diskussion beruhte auf der freien Stringtheorie. Wechselwirkungen werden durch
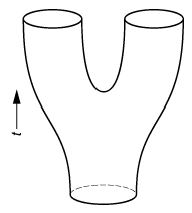
topologisch nicht-triviale Weltflächen berücksichtigt. [39]Abb. 3 zeigt den Zerfall eines
geschlossenen Strings in zwei geschlossene Strings als Beispiel.
Die Stärke der
Wechselwirkung wird durch die dimensionslose Stringkopplungskonstante ![]() kontrolliert. Sie ist dynamisch durch den
Hintergrundswert (Vakuumerwartungswert)
kontrolliert. Sie ist dynamisch durch den
Hintergrundswert (Vakuumerwartungswert) ![]() des Dilatons
des Dilatons ![]() , das wie das
Graviton zum masselosen Spektrum jeder Stringtheorie gehört, bestimmt:
, das wie das
Graviton zum masselosen Spektrum jeder Stringtheorie gehört, bestimmt: ![]() . Verschiedene
Werte von
. Verschiedene
Werte von ![]() entsprechen nicht verschiedenen Theorien,
sondern parametrisieren die Grundzustände einer Theorie. Die
Kopplungskonstanten der verschiedenen Stringtheorien sind jedoch a priori
voneinander unabhängig.
entsprechen nicht verschiedenen Theorien,
sondern parametrisieren die Grundzustände einer Theorie. Die
Kopplungskonstanten der verschiedenen Stringtheorien sind jedoch a priori
voneinander unabhängig.
Der quantenfeldtheoretischen Berechnung von Streuamplituden durch Summation über Feynman-Diagramme entspricht in der Stringtheorie die Summation über Weltflächen unterschiedlicher Topologie. Die erlaubten Topologien hängen dabei von der jeweiligen Stringtheorie ab. Insbesondere müssen für Typ-I-Theorien orientierbare und nicht-orientierbare Weltflächen berücksichtigt werden, während die Weltflächen der übrigen Stringtheorien orientierbar sind.
Die Berechnung der
Streuamplituden ![]() ist störungstheoretisch möglich.
ist störungstheoretisch möglich. ![]() wird in eine Potenzreihe in
wird in eine Potenzreihe in ![]() entwickelt,
entwickelt,
![]()
und jeder Term ![]() separat bestimmt. Die Gültigkeit der
Störungstheorie erfordert
separat bestimmt. Die Gültigkeit der
Störungstheorie erfordert ![]() . Die Potenz
von
. Die Potenz
von ![]() , zu der eine
Weltfläche beiträgt, ist durch ihre Euler-Zahl (und damit ihre Topologie)
bestimmt. Die Streuamplituden
, zu der eine
Weltfläche beiträgt, ist durch ihre Euler-Zahl (und damit ihre Topologie)
bestimmt. Die Streuamplituden ![]() physikalischer Zustände sind
Korrelationsfunktionen BRS-invarianter Vertexoperatoren in der durch die
Poljakow-Wirkung definierten zweidimensionalen Quantenfeldtheorie auf der
Weltfläche. In der Pfadintegral-Formulierung muss man a priori sowohl über alle
Metriken
physikalischer Zustände sind
Korrelationsfunktionen BRS-invarianter Vertexoperatoren in der durch die
Poljakow-Wirkung definierten zweidimensionalen Quantenfeldtheorie auf der
Weltfläche. In der Pfadintegral-Formulierung muss man a priori sowohl über alle
Metriken ![]() auf
auf ![]() als auch über alle Einbettungen
als auch über alle Einbettungen ![]() der Weltfläche in die Raumzeit integrieren.
Die Berechnung der Streuamplituden lässt sich am einfachsten mit den Methoden
der konformen Feldtheorie durchführen. Mit Hilfe der lokalen Symmetrien geht
man zur konformen Eichung über, und die unendlichdimensionale Integration über
die
der Weltfläche in die Raumzeit integrieren.
Die Berechnung der Streuamplituden lässt sich am einfachsten mit den Methoden
der konformen Feldtheorie durchführen. Mit Hilfe der lokalen Symmetrien geht
man zur konformen Eichung über, und die unendlichdimensionale Integration über
die ![]() reduziert sich auf eine endlichdimensionale
Integration über die modularen Parameter der Fläche
reduziert sich auf eine endlichdimensionale
Integration über die modularen Parameter der Fläche ![]() und eine Integration über die
Fadejew-Popow-Geisterfelder
und eine Integration über die
Fadejew-Popow-Geisterfelder ![]() . Für
geschlossene Strings schränkt die Forderung nach Invarianz auch unter solchen
Reparametrisierungen, die nicht kontinuierlich mit der Identitätstransformation
verbunden sind, den Integrationsbereich der modularen Parameter auf eine
fundamentale Region ein. Diese modulare Invarianz der Ein-Schleifen-Amplituden
garantiert die Anomaliefreiheit des Raumzeit-Spektrums. Für offene Strings
übernimmt die tadpole-cancellation-Bedingung diese Rolle.
. Für
geschlossene Strings schränkt die Forderung nach Invarianz auch unter solchen
Reparametrisierungen, die nicht kontinuierlich mit der Identitätstransformation
verbunden sind, den Integrationsbereich der modularen Parameter auf eine
fundamentale Region ein. Diese modulare Invarianz der Ein-Schleifen-Amplituden
garantiert die Anomaliefreiheit des Raumzeit-Spektrums. Für offene Strings
übernimmt die tadpole-cancellation-Bedingung diese Rolle.
Für Streuimpulse, die
klein sind gegenüber der charakteristischen Skala ![]() stimmen die Streuamplituden mit denen einer
effektiven Feldtheorie überein. Die Entwicklung der Streuamplituden in
stimmen die Streuamplituden mit denen einer
effektiven Feldtheorie überein. Die Entwicklung der Streuamplituden in ![]() entspricht einer Entwicklung der effektiven
Wirkung in Potenzen von Ableitungen. In führender Ordnung in
entspricht einer Entwicklung der effektiven
Wirkung in Potenzen von Ableitungen. In führender Ordnung in ![]() ist die effektive Niederenergie-Wirkung jeder
der fünf Stringtheorien gerade die Wirkung der jeweiligen klassischen
Supergravitationstheorie. Die Kopplungskonstanten der Supergravitation (die
10-dimensionale Gravitationskonstante
ist die effektive Niederenergie-Wirkung jeder
der fünf Stringtheorien gerade die Wirkung der jeweiligen klassischen
Supergravitationstheorie. Die Kopplungskonstanten der Supergravitation (die
10-dimensionale Gravitationskonstante ![]() und die 10-dimensionale Yang-Mills-Kopplung
und die 10-dimensionale Yang-Mills-Kopplung ![]() ) sind mit
) sind mit ![]() und
und ![]() über die Relationen
über die Relationen ![]() und
und ![]() (heterotischer String) bzw.
(heterotischer String) bzw. ![]() (Typ-I-String) verknüpft. Die Korrekturen in
(Typ-I-String) verknüpft. Die Korrekturen in ![]() führen u.a. zu einer Modifikation der
Einstein-Hilbert-Wirkung durch höhere Potenzen des Riemannschen
Krümmungstensors.
führen u.a. zu einer Modifikation der
Einstein-Hilbert-Wirkung durch höhere Potenzen des Riemannschen
Krümmungstensors.
Im Ultravioletten,
d.h. für Streuimpulse ![]() , wird die
endliche Ausdehnung des Strings relevant, und Abweichungen von
Quantenfeldtheorien werden bemerkbar. So sind, im Gegensatz zur
Quantenfeldtheorie, die Streuamplituden der Stringtheorie UV-endlich. Dieses
Verhalten kann man heuristisch anhand der im Vergleich zur Feldtheorie
»ausgedehnten« Feynman-Diagramme der Stringtheorie verstehen. Im Gegensatz zu
den Diagrammen der Quantenfeldtheorie gibt es keine punktförmigen
Wechselwirkungsvertizes mehr, die Wechselwirkung ist vielmehr »verschmiert«.
Die perturbative Endlichkeit der Stringtheorie ist letztendlich eine Konsequenz
der Tatsache, dass der String unendlich viele Anregungsmoden hat, die als
Zwischenzustände in Streuamplituden auftreten können. Im Rahmen der
Stringtheorie können nun z.B. störungstheoretische Quantenkorrekturen zur
Gravitationswechselwirkung berechnet werden. In diesem Sinne ist die
Stringtheorie (in ihrer supersymmetrischen Erweiterung) eine
ultraviolett-endliche und unitäre perturbative Quantengravitationstheorie.
, wird die
endliche Ausdehnung des Strings relevant, und Abweichungen von
Quantenfeldtheorien werden bemerkbar. So sind, im Gegensatz zur
Quantenfeldtheorie, die Streuamplituden der Stringtheorie UV-endlich. Dieses
Verhalten kann man heuristisch anhand der im Vergleich zur Feldtheorie
»ausgedehnten« Feynman-Diagramme der Stringtheorie verstehen. Im Gegensatz zu
den Diagrammen der Quantenfeldtheorie gibt es keine punktförmigen
Wechselwirkungsvertizes mehr, die Wechselwirkung ist vielmehr »verschmiert«.
Die perturbative Endlichkeit der Stringtheorie ist letztendlich eine Konsequenz
der Tatsache, dass der String unendlich viele Anregungsmoden hat, die als
Zwischenzustände in Streuamplituden auftreten können. Im Rahmen der
Stringtheorie können nun z.B. störungstheoretische Quantenkorrekturen zur
Gravitationswechselwirkung berechnet werden. In diesem Sinne ist die
Stringtheorie (in ihrer supersymmetrischen Erweiterung) eine
ultraviolett-endliche und unitäre perturbative Quantengravitationstheorie.
4 Kompaktifizierung
Die bisherige
Diskussion war auf Stringtheorien in einer vorgegebenen ![]() -dimensionalen
Minkowski-Raumzeit mit Metrik
-dimensionalen
Minkowski-Raumzeit mit Metrik ![]() beschränkt. Es ist aber möglich, eine
Stringtheorie in einer topologisch und metrisch nicht-trivialen Raumzeit zu
formulieren, in der z.B. nur
beschränkt. Es ist aber möglich, eine
Stringtheorie in einer topologisch und metrisch nicht-trivialen Raumzeit zu
formulieren, in der z.B. nur ![]() Dimensionen von unendlicher und die
verbleibenden
Dimensionen von unendlicher und die
verbleibenden ![]() Dimensionen von endlicher Ausdehnung sind.
Eine mögliche Realisierung einer solchen Kompaktifizierung beginnt mit dem
Faktorisierungsansatz
Dimensionen von endlicher Ausdehnung sind.
Eine mögliche Realisierung einer solchen Kompaktifizierung beginnt mit dem
Faktorisierungsansatz ![]() für die zehndimensionale Raumzeit. Hier ist
für die zehndimensionale Raumzeit. Hier ist ![]() der
der ![]() -dimensionale
Minkowski-Raum und
-dimensionale
Minkowski-Raum und ![]() eine
eine ![]() -dimensionale
kompakte Mannigfaltigkeit. In der Poljakow-Wirkung entspricht dies der
Ersetzung von
-dimensionale
kompakte Mannigfaltigkeit. In der Poljakow-Wirkung entspricht dies der
Ersetzung von ![]() durch die Metrik
durch die Metrik ![]() des Produktraumes
des Produktraumes ![]() , wodurch man
ein zweidimensionales nichtlineares Sigma-Modell mit Zielraum
, wodurch man
ein zweidimensionales nichtlineares Sigma-Modell mit Zielraum ![]() erhält. Die Konsistenz der Kompaktifizierung
verlangt ein konform invariantes Sigma-Modell und impliziert somit starke
Einschränkungen an
erhält. Die Konsistenz der Kompaktifizierung
verlangt ein konform invariantes Sigma-Modell und impliziert somit starke
Einschränkungen an ![]() . Die
resultierende
. Die
resultierende ![]() -dimensionale
Theorie hängt von Geometrie und Topologie der kompakten Mannigfaltigkeit ab.
Z.B. erhält man eine
-dimensionale
Theorie hängt von Geometrie und Topologie der kompakten Mannigfaltigkeit ab.
Z.B. erhält man eine ![]() -dimensionale
supersymmetrische Theorie nur für solche
-dimensionale
supersymmetrische Theorie nur für solche ![]() , auf denen
Killing-Spinoren existieren. Allgemein wird eine Kompaktifizierung nicht nur
durch die Metrik auf
, auf denen
Killing-Spinoren existieren. Allgemein wird eine Kompaktifizierung nicht nur
durch die Metrik auf ![]() , sondern
zusätzlich durch nicht-triviale Hintergrundswerte anderer masseloser
bosonischer Felder spezifiziert.
, sondern
zusätzlich durch nicht-triviale Hintergrundswerte anderer masseloser
bosonischer Felder spezifiziert.
Die einfachste
konsistente Kompaktifizierung des geschlossenen Strings ist auf einem Kreis ![]() mit Radius
mit Radius ![]() möglich. Dafür verlangt man
möglich. Dafür verlangt man ![]() , für eine der
Koordinaten. Dadurch entstehen zusätzliche masselose und massive Zustände: zum
einen die Kaluza-Klein-Anregungen mit
, für eine der
Koordinaten. Dadurch entstehen zusätzliche masselose und massive Zustände: zum
einen die Kaluza-Klein-Anregungen mit ![]() , die für
, die für ![]() entkoppeln, und zum anderen Windungszustände
mit
entkoppeln, und zum anderen Windungszustände
mit ![]() , die für
, die für ![]() masselos werden. Diese Windungszustände sind
charakteristisch für die Stringtheorie und treten in kompaktifizierten
Feldtheorien nicht auf. Sie führen zu einer Symmetrie des Spektrums und der
Streuamplituden des bosonischen Strings unter der T-Dualitätstransformation
masselos werden. Diese Windungszustände sind
charakteristisch für die Stringtheorie und treten in kompaktifizierten
Feldtheorien nicht auf. Sie führen zu einer Symmetrie des Spektrums und der
Streuamplituden des bosonischen Strings unter der T-Dualitätstransformation ![]() ,
, ![]() , bei der Kaluza-Klein-
und Windungszustände ihre Rollen vertauschen. Es entsprechen also geometrisch
verschiedene Kompaktifizierungen physikalisch identischen perturbativen
Grundzuständen der Stringtheorie. Diese Symmetrie legt es nahe,
, bei der Kaluza-Klein-
und Windungszustände ihre Rollen vertauschen. Es entsprechen also geometrisch
verschiedene Kompaktifizierungen physikalisch identischen perturbativen
Grundzuständen der Stringtheorie. Diese Symmetrie legt es nahe, ![]() als eine Minimallänge der Stringtheorie zu
interpretieren: Kompaktifizierung auf einem grossen Kreis ist ununterscheidbar
von der Kompaktifizierung auf einem kleinen Kreis. In beiden Fällen erhält man
im Limes
als eine Minimallänge der Stringtheorie zu
interpretieren: Kompaktifizierung auf einem grossen Kreis ist ununterscheidbar
von der Kompaktifizierung auf einem kleinen Kreis. In beiden Fällen erhält man
im Limes ![]() bzw.
bzw. ![]() ein Kontinuum von masselosen Zuständen, was
man als die Dekompaktifizierung einer zusätzlichen Dimension interpretiert.
Durch die Kompaktifizierung auf
ein Kontinuum von masselosen Zuständen, was
man als die Dekompaktifizierung einer zusätzlichen Dimension interpretiert.
Durch die Kompaktifizierung auf ![]() ensteht ein zusätzlicher freier Parameter, der
Radius
ensteht ein zusätzlicher freier Parameter, der
Radius ![]() des Kreises. Ähnlich wie die Stringkopplung
des Kreises. Ähnlich wie die Stringkopplung ![]() kann er als der (unbestimmte)
Vakuumerwartungswert eines masselosen skalaren Feldes (Modulus) aufgefasst
werden. Die Grundzustände der kompaktifizierten Theorie sind durch die
T-Dualität auf eine der beiden physikalisch äquivalenten fundamentalen Regionen
kann er als der (unbestimmte)
Vakuumerwartungswert eines masselosen skalaren Feldes (Modulus) aufgefasst
werden. Die Grundzustände der kompaktifizierten Theorie sind durch die
T-Dualität auf eine der beiden physikalisch äquivalenten fundamentalen Regionen
![]() oder
oder ![]() beschränkt. Während die T-Dualität eine
Symmetrie des bosonischen Strings ist, ist dies für die Typ-II-Theorien nicht
der Fall: hier transformiert die T-Dualität die Typ-IIA-Theorie auf
beschränkt. Während die T-Dualität eine
Symmetrie des bosonischen Strings ist, ist dies für die Typ-II-Theorien nicht
der Fall: hier transformiert die T-Dualität die Typ-IIA-Theorie auf ![]() in die Typ-IIB-Theorie auf
in die Typ-IIB-Theorie auf ![]() .
.
Eine einfache
Verallgemeinerung der Kompaktifizierung auf dem Kreis ist die Kompaktifizierung
auf einem ![]() -dimensionalen
Torus
-dimensionalen
Torus ![]() . Hier ist die
T-Dualität eine nicht-abelsche diskrete Symmetrie auf dem Parameterraum
(Moduliraum) der Kompaktifizierung, der u.a. durch die Komponenten der Metrik
auf
. Hier ist die
T-Dualität eine nicht-abelsche diskrete Symmetrie auf dem Parameterraum
(Moduliraum) der Kompaktifizierung, der u.a. durch die Komponenten der Metrik
auf ![]() aufgespannt wird.
aufgespannt wird.
Physikalisch
interessant ist der Fall ![]() . Für die Typ-II-Theorien
führt die Kompaktifizierung auf
. Für die Typ-II-Theorien
führt die Kompaktifizierung auf ![]() , auf dem
Niveau der niederenergetischen effektiven Wirkung zur
, auf dem
Niveau der niederenergetischen effektiven Wirkung zur ![]() -Supergravitation
und für die Typ-I- und die beiden heterotischen Theorien zur
-Supergravitation
und für die Typ-I- und die beiden heterotischen Theorien zur ![]() -Super-Yang-Mills
(SYM)-Theorie gekoppelt an
-Super-Yang-Mills
(SYM)-Theorie gekoppelt an ![]() -Supergravitation.
-Supergravitation.
![]() -Supersymmetrie
erhält man durch Kompaktifizierung des heterotischen Strings auf
sechsdimensionalen Calabi-Yau-Mannigfaltigkeiten. Die Vielzahl topologisch
verschiedener Calabi-Yau-Mannigfaltigkeiten führt zu einer Vielfalt
vierdimensionaler Anregungspektren. Dies ergibt verschiedene effektive
Niederenergietheorien, die sich u.a. durch Eichgruppe, masseloses Spektrum und
Wechselwirkungen voneinander unterscheiden. Auch in diesen Kompaktifizierungen
werden Grösse und Form der Calabi-Yau-Mannigfaltigkeit durch die
(störungstheoretisch) unbestimmten Vakuumerwartungswerte eichneutraler
Skalarfelder, der Modulifelder, parametrisiert.
-Supersymmetrie
erhält man durch Kompaktifizierung des heterotischen Strings auf
sechsdimensionalen Calabi-Yau-Mannigfaltigkeiten. Die Vielzahl topologisch
verschiedener Calabi-Yau-Mannigfaltigkeiten führt zu einer Vielfalt
vierdimensionaler Anregungspektren. Dies ergibt verschiedene effektive
Niederenergietheorien, die sich u.a. durch Eichgruppe, masseloses Spektrum und
Wechselwirkungen voneinander unterscheiden. Auch in diesen Kompaktifizierungen
werden Grösse und Form der Calabi-Yau-Mannigfaltigkeit durch die
(störungstheoretisch) unbestimmten Vakuumerwartungswerte eichneutraler
Skalarfelder, der Modulifelder, parametrisiert.
Allgemein bezeichnet man diskrete Symmetrien, die auf den Moduli einer Kompaktifizierung wirken und exakt in jeder Ordnung der Störungstheorie sind, als T-Dualität. Die mirror symmetry der Calabi-Yau-Kompaktifizierungen ist ein nicht-triviales Beispiel einer T-Dualität.
In der Sprache der
konformen Feldtheorie besteht die Kompaktifizierung der Superstringtheorien
darin, dass man ![]() freie Superfelder
freie Superfelder ![]() durch ein superkonformes nicht-lineares
Sigma-Modell mit Zielraum
durch ein superkonformes nicht-lineares
Sigma-Modell mit Zielraum ![]() und der selben zentralen Ladung ersetzt.
Allgemeiner kann man jedoch eine »interne« superkonforme Feldtheorie derselben
zentralen Ladung wählen, solange sie Konsistenzbedingungen wie z.B. modulare
Invarianz erfüllt. Eine solche Theorie hat i.a. keine Formulierung als
Sigma-Modell und lässt somit auch keine geometrische Interpretation zu. Eine
analoge Diskussion gilt auch für die heterotischen Theorien, wobei dann auch
die Beiträge der zusätzlichen Felder
und der selben zentralen Ladung ersetzt.
Allgemeiner kann man jedoch eine »interne« superkonforme Feldtheorie derselben
zentralen Ladung wählen, solange sie Konsistenzbedingungen wie z.B. modulare
Invarianz erfüllt. Eine solche Theorie hat i.a. keine Formulierung als
Sigma-Modell und lässt somit auch keine geometrische Interpretation zu. Eine
analoge Diskussion gilt auch für die heterotischen Theorien, wobei dann auch
die Beiträge der zusätzlichen Felder ![]() bzw.
bzw. ![]() berücksichtigt werden müssen.
berücksichtigt werden müssen.
5 Dualität
Die bisher vorgestellte Formulierung der Stringtheorie beschreibt die störungstheoretische Quantisierung eines Strings, der sich in einem vorgegebenen, klassischen Raumzeithintergrund bewegt. Eine vollständige Theorie der Quantengravitation sollte jedoch auch diesen Raumzeithintergrund dynamisch generieren. Diesen Anspruch kann die Stringtheorie bisher nicht erfüllen, u.a. auch wegen ihrer bislang ausschliesslich störungstheoretischen Formulierung. Meist werden störungstheoretische Methoden zur approximativen Berechnung physikalischer Grössen einer zumindest im Prinzip bekannten Theorie benutzt. In der Stringtheorie ist die Situation eine andere: hier ist lediglich eine störungstheoretische Entwicklung bekannt, wohingegen eine fundamentale Formulierung der Stringtheorie, die zu dieser Störungsreihe führt, noch fehlt.
Einen Zugang zu
nichtstörungstheoretischer Information eröffnet die aus supersymmetrischen
Quantenfeldtheorien bekannte Dualität zwischen stark und schwach gekoppelten
Theorien. Sie ermöglicht es, Bereiche starker Kopplung einer gegebenen Theorie
mit perturbativen Methoden in der dualen Theorie zu kontrollieren. Die
zueinander dualen Theorien können störungstheoretisch sehr unterschiedlich sein
und sich z.B. in ihren Freiheitsgraden und Symmetrien voneinander
unterscheiden. So können die störungstheoretischen Freiheitsgrade der einen
Theorie Solitonen, also lokalisierte Lösungen der klassischen
Bewegungsgleichungen, der (schwach gekoppelten) dualen Theorie sein. Diese
gehören zum nichtperturbativen Spektrum, da ihre Massen für ![]() divergieren und die Zustände somit entkoppeln.
Falls die Solitonen bei starker Kopplung, d.h.
divergieren und die Zustände somit entkoppeln.
Falls die Solitonen bei starker Kopplung, d.h. ![]() , sehr leicht
werden und schwach gekoppelt sind, übernehmen sie in der dualen Theorie die
Rolle der elementaren Anregungen. Die Dualität zwischen stark und schwach
gekoppelten Theorien bezeichnet man als S-Dualität.
, sehr leicht
werden und schwach gekoppelt sind, übernehmen sie in der dualen Theorie die
Rolle der elementaren Anregungen. Die Dualität zwischen stark und schwach
gekoppelten Theorien bezeichnet man als S-Dualität.
Die S-Dualität ist
nicht-perturbativ im Sinne einer Entwicklung in der Kopplungskonstanten ![]() , aber
perturbativ in einer Entwicklung in
, aber
perturbativ in einer Entwicklung in ![]() . Für die
T-Dualität sind diese Sachverhalte gerade vertauscht. Von U-Dualität spricht
man, wenn diskrete Symmetrien vorliegen, die weder in
. Für die
T-Dualität sind diese Sachverhalte gerade vertauscht. Von U-Dualität spricht
man, wenn diskrete Symmetrien vorliegen, die weder in ![]() noch in
noch in ![]() perturbativ sind.
perturbativ sind.
Der Beweis der S-Dualität (oder U-Dualität) ist schwierig, da er eine nicht-störungstheoretische Formulierung der Feld- und Stringtheorie voraussetzt. Man kann aber die Dualitätshypothese an solchen solitonischen Zuständen überprüfen, deren Quantenkorrekturen unter Kontrolle sind und deren Massen als Funktionen der Kopplungskonstanten bei schwacher Kopplung vollständig bestimmt werden können. Für diese Zustände ist eine Extrapolation in den Bereich starker Kopplung zulässig, und ein Vergleich mit den störungstheoretischen Zuständen der dualen Theorie wird möglich. Solche Zustände existieren in Feld- bzw. Stringtheorien mit erweiterter Supersymmetrie und werden als Bogomolny-Prasad-Sommerfield (BPS)-Zustände bezeichnet. Sie sind dadurch ausgezeichnet, dass sie einen Teil der Supersymmetrie erhalten.
Zum BPS-Spektrum der
Stringtheorie gehören insbesondere die D-Branes. In Analogie zur Kopplung
elektrisch geladener Teilchen an das Maxwell-Potential ![]() koppelt eine »elektrische« p-dimensionale Dp-Brane an
ein
koppelt eine »elektrische« p-dimensionale Dp-Brane an
ein ![]() -Form-Potential
-Form-Potential
![]() . Ausser den
elektrisch geladenen gibt es auch »magnetisch« geladene Branes. Sie sind durch
den zu
. Ausser den
elektrisch geladenen gibt es auch »magnetisch« geladene Branes. Sie sind durch
den zu ![]() dualen Feldstärketensor
dualen Feldstärketensor ![]() charakterisiert. Somit ist das zu einer
elektrischen Dp-Brane duale (im Sinne von
Hodge-Dualität) magnetisch geladene Objekt eine (6 - p)-dimensionale
D(6 -
p)-Brane. Die Potentiale
charakterisiert. Somit ist das zu einer
elektrischen Dp-Brane duale (im Sinne von
Hodge-Dualität) magnetisch geladene Objekt eine (6 - p)-dimensionale
D(6 -
p)-Brane. Die Potentiale ![]() , an die die
D-Branes koppeln, sind gerade die masselosen Felder in den (R,R)-Sektoren der
Superstringtheorien (vgl. Tabelle 1). Das führt zu den D-Brane-Spektren in
Tabelle 2.
, an die die
D-Branes koppeln, sind gerade die masselosen Felder in den (R,R)-Sektoren der
Superstringtheorien (vgl. Tabelle 1). Das führt zu den D-Brane-Spektren in
Tabelle 2.
Antisymmetrische
Tensorfelder kommen auch im (NS,NS)-Sektor vor. Der fundamentale String (F1)
koppelt an ![]() , und das duale
magnetische Objekt ist fünfdimensional und wird als NS5-Brane bezeichnet.
, und das duale
magnetische Objekt ist fünfdimensional und wird als NS5-Brane bezeichnet.
Branes wurden zunächst
als klassische Lösungen der effektiven Supergravitationstheorien gefunden und
erhielten dann eine stringspezifische Interpretation als die bereits oben
eingeführten dynamischen D-Branes, an die offene Strings Raumzeit-Impuls
abgeben können. Die Supergravitationslösungen beschreiben ausgedehnte Objekte
und enthalten ausser einer nicht-trivialen Raumzeit-Metrik und dem Dilaton eine
nicht-verschwindende ![]() -Form
(Feldstärke). Die aus diesen Lösungen berechnete Spannung (Energiedichte) für
den F1-String ist unabhängig von der jeweiligen String-Kopplungskonstante.
Dahingegen verhält sich die Energiedichte der NS5-Brane wie
-Form
(Feldstärke). Die aus diesen Lösungen berechnete Spannung (Energiedichte) für
den F1-String ist unabhängig von der jeweiligen String-Kopplungskonstante.
Dahingegen verhält sich die Energiedichte der NS5-Brane wie ![]() und die der D-Branes wie
und die der D-Branes wie ![]() . Bei schwacher
Kopplung sind also sowohl die D-Branes als auch die NS5-Brane schwer und
entkoppeln im Grenzwert
. Bei schwacher
Kopplung sind also sowohl die D-Branes als auch die NS5-Brane schwer und
entkoppeln im Grenzwert ![]() . Sie gehören
zum nicht-perturbativen Sektor der jeweiligen perturbativ definierten
Stringtheorie. Bei starker Kopplung,
. Sie gehören
zum nicht-perturbativen Sektor der jeweiligen perturbativ definierten
Stringtheorie. Bei starker Kopplung, ![]() , werden die
BPS-p-Branes leicht und können in manchen Fällen als die fundamentalen Objekte
der dualen Theorie, die jetzt eine Störungsreihe in
, werden die
BPS-p-Branes leicht und können in manchen Fällen als die fundamentalen Objekte
der dualen Theorie, die jetzt eine Störungsreihe in ![]() besitzt, interpretiert werden.
besitzt, interpretiert werden.
Ein Beispiel in ![]() ist die S-Dualität zwischen dem heterotischen
SO(32)-String und dem Typ-I-String. Die Kopplungskonstanten dieser beiden
Theorien sind invers zueinander, und der D-String der Typ-I-Theorie wird im
Limes starker Typ-I-Kopplung auf den fundamentalen heterotischen String
abgebildet.
ist die S-Dualität zwischen dem heterotischen
SO(32)-String und dem Typ-I-String. Die Kopplungskonstanten dieser beiden
Theorien sind invers zueinander, und der D-String der Typ-I-Theorie wird im
Limes starker Typ-I-Kopplung auf den fundamentalen heterotischen String
abgebildet.
Die Typ-IIB-Theorie in
![]() hat sowohl einen fundamentalen als auch einen
D-String. Ihre Energiedichten verhalten sich wie
hat sowohl einen fundamentalen als auch einen
D-String. Ihre Energiedichten verhalten sich wie ![]() , d.h. bei
starker Kopplung ist der D-String sehr viel leichter als der F-String. Die
Typ-IIB-Theorie ist selbst-dual unter S-Dualität, d.h. invariant unter
, d.h. bei
starker Kopplung ist der D-String sehr viel leichter als der F-String. Die
Typ-IIB-Theorie ist selbst-dual unter S-Dualität, d.h. invariant unter ![]() und gleichzeitigem Vertauschen von F- und
D-String. Über T-Dualität ist die Typ-IIB-Theorie mit der Typ-IIA-Theorie
verbunden. T-Dualität verbindet auch die beiden heterotischen Theorien.
und gleichzeitigem Vertauschen von F- und
D-String. Über T-Dualität ist die Typ-IIB-Theorie mit der Typ-IIA-Theorie
verbunden. T-Dualität verbindet auch die beiden heterotischen Theorien.
Die Typ-IIA-Theorie
besitzt gebundene BPS-Zustände von ![]() D0-Branes mit Masse
D0-Branes mit Masse ![]() . Diese
Zustände können als Kaluza-Klein-Anregungen einer auf
. Diese
Zustände können als Kaluza-Klein-Anregungen einer auf ![]() kompaktifizierten Theorie mit Radius
kompaktifizierten Theorie mit Radius ![]() interpretiert werden. Im Limes
interpretiert werden. Im Limes ![]() besitzt die Typ-IIA-Theorie elfdimensionale
Poincaré-Invarianz. Die masselosen Freiheitsgrade und ihre Wechselwirkungen
werden bei niedrigen Energien durch die elfdimensionale Supergravitation
beschrieben. Mit
besitzt die Typ-IIA-Theorie elfdimensionale
Poincaré-Invarianz. Die masselosen Freiheitsgrade und ihre Wechselwirkungen
werden bei niedrigen Energien durch die elfdimensionale Supergravitation
beschrieben. Mit ![]() ergibt sich ihre charakteristische Skala zu
ergibt sich ihre charakteristische Skala zu ![]() . Bei Energien
. Bei Energien ![]() liefert weder die Stringtheorie noch die
Supergravitation eine adäquate Beschreibung. Der noch unbekannten Theorie, die
dies bewerkstelligt, hat man den Namen M-Theorie gegeben. Auch der stark
gekoppelte E8 ´ E8-heterotische String
kann als Kompaktifizierung diesmal auf einem Intervall der Länge
liefert weder die Stringtheorie noch die
Supergravitation eine adäquate Beschreibung. Der noch unbekannten Theorie, die
dies bewerkstelligt, hat man den Namen M-Theorie gegeben. Auch der stark
gekoppelte E8 ´ E8-heterotische String
kann als Kompaktifizierung diesmal auf einem Intervall der Länge ![]() dieser M-Theorie interpretiert werden. Je
ein E8-Faktor
ist auf einem der beiden zehndimensionalen Ränder lokalisiert.
dieser M-Theorie interpretiert werden. Je
ein E8-Faktor
ist auf einem der beiden zehndimensionalen Ränder lokalisiert.
Die
Dualitätsrelationen implizieren, dass alle fünf Stringtheorien lediglich
verschiedene störungstheoretische Approximationen ein und derselben
fundamentalen Theorie sind. Das Auftreten der elfdimensionalen Supergravitation
bedeutet, dass die fünf Stringtheorien keine komplette Beschreibung im Bereich
starker Kopplung liefern können. Die hypothetische Theorie, aus der sich sowohl
die Stringtheorien als auch die elfdimensionale Supergravitationstheorie in
verschiedenen Näherungen ableiten lassen, ist die schon erwähnte M-Theorie. Die
elementaren Anregungen dieser Theorie hängen von der gewählten Approximation
ab. Als elfdimensionale Theorie besitzt sie Membranen (M2-Branes) und deren
duale Objekte, M5-Branes. Dann lässt sich z.B. der fundamentale String der
Typ-IIA-Theorie als eine M2-Brane, deren eine Dimension um den Kreis mit Radius
![]() gewickelt ist, interpretieren.
gewickelt ist, interpretieren.
Ausser den bisher beschriebenen Dualitätsrelationen gibt es noch viele weitere Beziehungen zwischen den verschiedenen Stringtheorien, sowohl in ihrer kritischen Dimension als auch nach der Kompaktifizierung. Bei allen nicht-perturbativen Dualitäten spielen Branes eine zentrale Rolle.
In Anwesenheit von
D-Branes hat man ausser den Anregungsmoden des geschlossenen Strings auch
diejenigen des offenen Strings, dessen Endpunkte sich entlang der D-Branes
bewegen. So werden z.B. die masselosen Moden für ![]() deckungsgleiche D3-Branes bei niedrigen
Energien (
deckungsgleiche D3-Branes bei niedrigen
Energien (![]() ) durch eine
vierdimensionale
) durch eine
vierdimensionale ![]() -SYM-Theorie
mit Eichgruppe U(N) beschrieben. Diese Theorie ist
auf dem Weltvolumen der D3-Branes lokalisiert. Ihre Eichkopplungskonstante ist
-SYM-Theorie
mit Eichgruppe U(N) beschrieben. Diese Theorie ist
auf dem Weltvolumen der D3-Branes lokalisiert. Ihre Eichkopplungskonstante ist ![]() . Für
. Für ![]() entkoppeln die Moden des offenen Strings von
der Gravitation. Eine Vielzahl weiterer Theorien kann mit Hilfe geeignet
gewählter D-Brane-Konfigurationen konstruiert und untersucht werden. Besonders
hervorzuheben sind hier BPS-Konfigurationen, die mit extremalen Schwarzen
Löchern identiziert werden können. Für diese lässt sich die
Bekenstein-Hawking-Entropie durch Abzählen von Zuständen mikroskopisch
herleiten.
entkoppeln die Moden des offenen Strings von
der Gravitation. Eine Vielzahl weiterer Theorien kann mit Hilfe geeignet
gewählter D-Brane-Konfigurationen konstruiert und untersucht werden. Besonders
hervorzuheben sind hier BPS-Konfigurationen, die mit extremalen Schwarzen
Löchern identiziert werden können. Für diese lässt sich die
Bekenstein-Hawking-Entropie durch Abzählen von Zuständen mikroskopisch
herleiten.
Eine etwas anders
geartete Dualität ergibt sich, wenn man die beiden Beschreibungen von D3-Branes
miteinander vergleicht. Zum einen sind sie die möglichen Endpunkte offener
Strings. Bei niedrigen Energien erhält man für ![]() parallele, flache, unendlich ausgedehnte
D3-Branes eine U(N)-SYM-Theorie mit
parallele, flache, unendlich ausgedehnte
D3-Branes eine U(N)-SYM-Theorie mit ![]() auf dem vierdimensionalen Weltvolumen, die von
der zehndimensionalen Gravitation entkoppelt ist. Alternativ findet man
dieselbe Brane-Konfiguration als klassische Lösung der Typ-IIB-Supergravitation,
die eine Verallgemeinerung der Reissner-Nordstrøm-Metrik ist. Hier findet man
bei niedrigen Energien die Entkopplung der asymptotisch flachen Region von dem
Bereich in der Nähe des Horizontes, wo die Metrik die des
auf dem vierdimensionalen Weltvolumen, die von
der zehndimensionalen Gravitation entkoppelt ist. Alternativ findet man
dieselbe Brane-Konfiguration als klassische Lösung der Typ-IIB-Supergravitation,
die eine Verallgemeinerung der Reissner-Nordstrøm-Metrik ist. Hier findet man
bei niedrigen Energien die Entkopplung der asymptotisch flachen Region von dem
Bereich in der Nähe des Horizontes, wo die Metrik die des ![]() -Produktraumes
ist. Ein Vergleich führt zu der Hypothese, dass die (
-Produktraumes
ist. Ein Vergleich führt zu der Hypothese, dass die (![]() )-U(N)-SYM-Theorie in vier Dimensionen dual zur
Typ-IIB-Supergravitation, kompaktifiziert auf
)-U(N)-SYM-Theorie in vier Dimensionen dual zur
Typ-IIB-Supergravitation, kompaktifiziert auf ![]() , ist.
Untersucht man die Gültigkeit der effektiven Beschreibung der
Typ-II-Stringtheorie durch die Supergravitation, findet man, dass
, ist.
Untersucht man die Gültigkeit der effektiven Beschreibung der
Typ-II-Stringtheorie durch die Supergravitation, findet man, dass ![]() mit
mit ![]() gelten muss.
gelten muss. ![]() ist die effektive Kopplungskonstante der
Eichtheorie. Es handelt sich damit um die Dualität zwischen einer schwach
gekoppelten Stringtheorie und einer stark gekoppelten Eichtheorie im large
N-Limes. Man erwartet, dass
ist die effektive Kopplungskonstante der
Eichtheorie. Es handelt sich damit um die Dualität zwischen einer schwach
gekoppelten Stringtheorie und einer stark gekoppelten Eichtheorie im large
N-Limes. Man erwartet, dass ![]() -Korrekturen
der Eichtheorie stringtheoretischen Korrekturen der Supergravitation
entsprechen. Diese Dualität wird durch den Vergleich der Symmetrien und durch
die Identifikation eichinvarianter Operatoren mit den Kaluza-Klein-Anregungen
auf dem
-Korrekturen
der Eichtheorie stringtheoretischen Korrekturen der Supergravitation
entsprechen. Diese Dualität wird durch den Vergleich der Symmetrien und durch
die Identifikation eichinvarianter Operatoren mit den Kaluza-Klein-Anregungen
auf dem ![]() -Hintergrund
gestützt.
-Hintergrund
gestützt.
Da die (![]() )-SYM-Theorie
eine konform invariante Quantenfeldtheorie ist, spricht man auch von einer
AdS/CFT-Korrespondenz. Andere Beispiele einer solchen Korrespondenz ergeben
sich z.B. durch die Kompaktifizierung der Typ-IIA-Theorie auf
)-SYM-Theorie
eine konform invariante Quantenfeldtheorie ist, spricht man auch von einer
AdS/CFT-Korrespondenz. Andere Beispiele einer solchen Korrespondenz ergeben
sich z.B. durch die Kompaktifizierung der Typ-IIA-Theorie auf ![]() . Diese
Geometrie entspricht einer Anordnung von D1- und D5-Branes, und die
Kompaktifizierung ist dual zu einer zweidimensionalen konformen Feldtheorie.
. Diese
Geometrie entspricht einer Anordnung von D1- und D5-Branes, und die
Kompaktifizierung ist dual zu einer zweidimensionalen konformen Feldtheorie.
Literatur
[1] M. Green, J. Schwarz, E. Witten, Superstring Theory, Vol. I+II, Cambridge University Press, 1987.
[2] D. Lüst, S. Theisen, Lectures on String Theory, Springer Verlag, 1989.
[3] J. Polchinski, String Theory, Vol. I+II, Cambridge University Press, 1998.
Stringtheorie
1: Bosonische masselose Felder in den Typ-II-Theorien, im
geschlossenen Stringsektor der Typ-I-Theorie und in den heterotischen Theorien.
![]() ist die Raumzeit-Metrik,
ist die Raumzeit-Metrik, ![]() ein antisymetrisches Tensorfeld und
ein antisymetrisches Tensorfeld und ![]() das Dilaton.
das Dilaton. ![]() ist das Vektorpotential der Eichgruppen E8 ´ E8 bzw. SO(32).
ist das Vektorpotential der Eichgruppen E8 ´ E8 bzw. SO(32). ![]() ist ein
ist ein ![]() -Form-Feld mit
Feldstärke
-Form-Feld mit
Feldstärke ![]() . Die
Feldstärke von
. Die
Feldstärke von ![]() ist selbst-dual,
ist selbst-dual, ![]() , und
, und ![]() ist eine nicht-propagierende
0-Form-Feldstärke.
ist eine nicht-propagierende
0-Form-Feldstärke.
|
Sektor |
(NS,NS) |
(R,R) |
|
Typ IIA |
|
|
|
Typ IIB |
|
|
|
Typ I |
|
|
|
heterotisch |
|
|
Stringtheorie
2: Die D(-1)-Brane der Typ-IIB-Theorie ist ein D-Instanton. Die
D9-Brane in Typ I ist entartet. Sie impliziert, dass sich offene Strings frei in
der zehndimensionalen Raumzeit bewegen können. Alle anderen D-Branes stehen in
1:1-Beziehung zu »elektrischen« (R,R)-Potentialen und deren dualen
»magnetischen« Potentialen. Die D-Branes koppeln an diese Potentiale als
elementare Quellen. Unter T-Dualität ändern sich die Randbedingungen der
offenen Strings, N![]() D, und somit
werden Dp-Branes in D(
D, und somit
werden Dp-Branes in D(![]() )-Branes
abgebildet, je nachdem ob die T-Dualität in einer Richtung entlang (-)
oder transversal (+) zum Weltvolumen der Brane durchgeführt wird.
)-Branes
abgebildet, je nachdem ob die T-Dualität in einer Richtung entlang (-)
oder transversal (+) zum Weltvolumen der Brane durchgeführt wird.
|
Dp-Branes |
p |
|
Typ IIA |
0,2,4,6,8 |
|
Typ IIB |
-1,1,3,5,7 |
|
Typ I |
1,5,9 |
Stringtheorie 1: Weltfläche eines freien a) offenen und b) geschlossenen Strings.
Stringtheorie 2: Offene Strings können auf D-Branes enden.
Stringtheorie 3: Zerfall eines geschlossenen Strings in zwei geschlossene Strings.
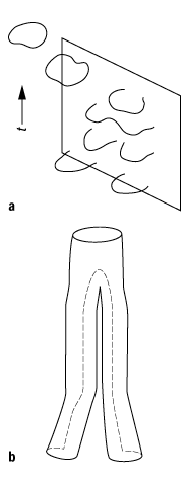
Stringtheorie 4: Zwei offene Strings vereinigen sich zu einem geschlossenen String im a) Raumzeitbild und b) als Weltflächendiagramm.
Stringtheorie 5: Einschleifen-Quantenkorrektur zur Propagation des geschlossenen Strings.