Supraleitung und Suprafluidität

Julian Schultheiss
Supraleitung, Tieftemperaturphysik und -technik
Dieses Essay befasst sich mit einer einheitlichen theoretischen Betrachtung der Supraleitung in Metallen und der Suprafluidität in elektrisch neutralen Fermisystemen. Es soll aufgezeigt werden, warum dieses faszinierende Phänomen auch heute noch fast ein Jahrhundert nach seiner experimentellen Entdeckung und fast ein halbes Jahrhundert nach seiner ersten theoretischen Deutung Gegenstand intensiver Forschung ist. Im ersten Abschnitt wird das völlig unterschiedliche Verhalten des Normalzustands dieser Systeme mit dem des Suprazustands kontrastiert und es werden einige wichtige Aspekte der historischen Entwicklung dieses Forschungsgebietes nachgezeichnet. Dann wird eine allgemeine Klassifizierung supraleitender und suprafluider Fermisysteme nach der Symmetrie ihres Grundzustands durchgeführt. Der nächste Abschnitt beschäftigt sich mit den Gleichgewichtseigenschaften dieser Systeme bei endlicher Temperatur. Schliesslich wird die Frage aufgeworfen, wie die Supraleitung und die Suprafluidität auf äussere Störungen reagiert und was man daraus über die innere Struktur und die Symmetrie der supraleitenden und superfluiden Phase lernen kann. Suprafluidität in Bosonen-Systemen wird an anderer Stelle behandelt (Suprafluidität).
1 Normal- und Suprazustand
In normalen Metallen
beruht der elektrische Widerstand auf der Streuung der Leitungselektronen an
thermischen Gitterschwingungen (Phononen) und an Gitterfehlern
(Verunreinigungen, Fehlstellen, Versetzungen, Korngrenzen, etc.), die durch
eine Streurate ![]() beschrieben wird. Die elektrische Stromdichte
beschrieben wird. Die elektrische Stromdichte ![]() relaxiert gemäss
relaxiert gemäss
![]()
Hier bezeichnen ![]() die Teilchendichte,
die Teilchendichte, ![]() und
und ![]() die elektronische Ladung und Masse. Die
treibende Kraft
die elektronische Ladung und Masse. Die
treibende Kraft ![]() ist die elektrische Feldstärke
ist die elektrische Feldstärke ![]() , die sich wie
üblich aus den elektromagnetischen Potentialen
, die sich wie
üblich aus den elektromagnetischen Potentialen ![]() und
und ![]() ableiten lässt. Die elektrische Leitfähigkeit
ableiten lässt. Die elektrische Leitfähigkeit ![]() charakterisiert den Zusammenhang zwischen
Stromdichte und elektrischem Feld:
charakterisiert den Zusammenhang zwischen
Stromdichte und elektrischem Feld:
![]()
Dieser Zusammenhang
ist als Drude-Gesetz (Drude-Lorenz-Theorie) bzw. als Ohmsches Gesetz bekannt.
Ihr Kehrwert, der elektrische Widerstand ![]() , ist
proportional zur Impulsrelaxationsrate
, ist
proportional zur Impulsrelaxationsrate ![]() . Im Grenzfall
. Im Grenzfall ![]() verschwinden die Phononen, und der
ausschliesslich durch Defekte verursachte (Rest-) Widerstand von sehr sauberen
Metallen kann sehr gering sein.
verschwinden die Phononen, und der
ausschliesslich durch Defekte verursachte (Rest-) Widerstand von sehr sauberen
Metallen kann sehr gering sein.
Im Jahre 1911
studierte Heike Kamerlingh Onnes in Leiden diese Effekte an Quecksilber im
Temperaturbereich zwischen 1 und 5 K. Er kam zu dem überraschenden Resultat,
dass der elektrische Widerstand ![]() , anstatt
stetig auf den Restwiderstandswert abzusinken, bei einer kritischen Temperatur Tc
= 4,2 K verschwand. Dieses Phänomen (
, anstatt
stetig auf den Restwiderstandswert abzusinken, bei einer kritischen Temperatur Tc
= 4,2 K verschwand. Dieses Phänomen (![]() ,
, ![]() ) wird seitdem
Supraleitung genannt. Die wohl beeindruckendste Konsequenz des
Supraleitungsphänomens demonstrierte Kamerlingh Onnes, indem er einen Strom in
einem supraleitenden Bleiring bei 4 K in Gang setzte, die Stromquelle
abschaltete und einen Dauerstrom (Dauerstrom, supraleitender) über ein ganzes
Jahr ohne messbare Reduktion beobachten konnte. Kamerlingh Onnes\' Entdeckung
wurde im Jahre 1913 mit dem Physik-Nobelpreis gewürdigt.
) wird seitdem
Supraleitung genannt. Die wohl beeindruckendste Konsequenz des
Supraleitungsphänomens demonstrierte Kamerlingh Onnes, indem er einen Strom in
einem supraleitenden Bleiring bei 4 K in Gang setzte, die Stromquelle
abschaltete und einen Dauerstrom (Dauerstrom, supraleitender) über ein ganzes
Jahr ohne messbare Reduktion beobachten konnte. Kamerlingh Onnes\' Entdeckung
wurde im Jahre 1913 mit dem Physik-Nobelpreis gewürdigt.
Dass das Phänomen der
Supraleitung noch mehr beinhaltet als das blosse Verschwinden des elektrischen
Widerstandes unterhalb einer Sprungtemperatur ![]() , zeigten
Walther Meissner und Robert Ochsenfeld im Jahre 1933. Sie entdeckten, dass
Supraleiter Magnetfelder reversibel aus ihrem Inneren verdrängen oder
abschirmen, und zwar unabhängig davon, ob man den Supraleiter im Magnetfeld
abkühlt (Verdrängungseffekt) oder erst unterhalb der Sprungtemperatur
, zeigten
Walther Meissner und Robert Ochsenfeld im Jahre 1933. Sie entdeckten, dass
Supraleiter Magnetfelder reversibel aus ihrem Inneren verdrängen oder
abschirmen, und zwar unabhängig davon, ob man den Supraleiter im Magnetfeld
abkühlt (Verdrängungseffekt) oder erst unterhalb der Sprungtemperatur ![]() ein Magnetfeld anlegt (Abschirmeffekt). Der
Supraleiter verhält sich somit wie ein idealer Diamagnet. Diese
Feldverdrängungseigenschaft der Supraleiter ist nach ihren Entdeckern
Meissner-Ochsenfeld-Effekt benannt geworden.
ein Magnetfeld anlegt (Abschirmeffekt). Der
Supraleiter verhält sich somit wie ein idealer Diamagnet. Diese
Feldverdrängungseigenschaft der Supraleiter ist nach ihren Entdeckern
Meissner-Ochsenfeld-Effekt benannt geworden.
Parallel zu dieser
Entdeckung entwickelten die Brüder Fritz und Heinz London, aber auch Max von
Laue, die phänomenologische sog. London-Laue-Theorie der Supraleitung
(1935-1938), in der eine makroskopische Anzahl supraleitender Teilchen der
Ladung ![]() und der Masse
und der Masse ![]() , die sich in
den elektromagnetischen Potentialen
, die sich in
den elektromagnetischen Potentialen ![]() und
und ![]() bewegen, durch eine kollektive
quantenmechanische Wellenfunktion
bewegen, durch eine kollektive
quantenmechanische Wellenfunktion ![]() mit Amplitude
mit Amplitude ![]() und Phase
und Phase ![]() beschrieben wird. Im Gegensatz zur
Interpretation der gewöhnlichen Quantenmechanik von
beschrieben wird. Im Gegensatz zur
Interpretation der gewöhnlichen Quantenmechanik von ![]() als Wahrscheinlichkeitsamplitude, ein Teilchen
am Ort
als Wahrscheinlichkeitsamplitude, ein Teilchen
am Ort ![]() zur Zeit
zur Zeit ![]() vorzufinden, wurde
vorzufinden, wurde ![]() mit der makroskopischen Teilchenzahldichte der
supraleitenden Ladungsträger verknüpft. Ansonsten konnten alle aus der
Quantenmechanik bekannten Resultate übernommen werden, insbesondere die
Tatsache, dass der Schrödinger-Gleichung für
mit der makroskopischen Teilchenzahldichte der
supraleitenden Ladungsträger verknüpft. Ansonsten konnten alle aus der
Quantenmechanik bekannten Resultate übernommen werden, insbesondere die
Tatsache, dass der Schrödinger-Gleichung für ![]() die Kontinuitätsgleichung für die
Kondensat-Dichte
die Kontinuitätsgleichung für die
Kondensat-Dichte ![]() äquivalent ist, in der die Ladungssuprastromdichte
äquivalent ist, in der die Ladungssuprastromdichte
![]() die Form
die Form
![]()
hat. Die einzelnen Ladungsträger verlieren somit ihre Individualität völlig, denn sie gehorchen kollektiv den Gesetzen der Quantenmechanik. Obwohl diese Theorie nichts über den Mechanismus, der zur Supraleitung führt, aussagt, betrachtet sie die Supraleitung erstmals als makroskopisches Quantenphänomen und kann Dauerströme, Magnetfeldabschirmung, charakterisiert durch die sog. Londonsche Magnetfeldeindringtiefe (Londonsche Theorie der Supraleitung)
![]()
sowie die sehr viel
später entdeckte Flussquantisierung durch einen Supraleiter vorhersagen. Wegen
der Eindeutigkeitsforderung ![]() , an
, an ![]() ergibt sich für das (Fluss-) Integral über die
Querschittsfläche
ergibt sich für das (Fluss-) Integral über die
Querschittsfläche ![]() eines supraleitenden Hohlzylinders die
Bedingung
eines supraleitenden Hohlzylinders die
Bedingung
![]()
in der ![]() und
und ![]() das Quantum des magnetischen Flusses
darstellt. Im Jahre 1961 gelang Robert Doll und Martin Näbauer (unabhängig
davon aber auch Deaver und Fairbanks) schliesslich der experimentelle Beweis
dafür, dass die Grösse
das Quantum des magnetischen Flusses
darstellt. Im Jahre 1961 gelang Robert Doll und Martin Näbauer (unabhängig
davon aber auch Deaver und Fairbanks) schliesslich der experimentelle Beweis
dafür, dass die Grösse ![]() quantisiert ist. Das experimentell bestimmte
Flussquantum liess den Schluss zu, dass beim Ladungstransport in Supraleitern
nicht, wie in der London-Theorie angenommen, einzelne (
quantisiert ist. Das experimentell bestimmte
Flussquantum liess den Schluss zu, dass beim Ladungstransport in Supraleitern
nicht, wie in der London-Theorie angenommen, einzelne (![]() ,
, ![]() ,
, ![]() ), sondern
Paare von Elektronen mit der doppelten Elementarladung (
), sondern
Paare von Elektronen mit der doppelten Elementarladung (![]() ,
, ![]() ,
, ![]() beteiligt sind.
beteiligt sind.
Wie die
Metallelektronen zeigen auch elektrisch neutrale Flüssigkeiten in ihrem
Normalzustand das Phänomen eines Strömungswiderstands. Die Massenstromdichte ![]() genügt der Relaxationsgleichung
genügt der Relaxationsgleichung
![]()
in der die treibende
Kraft ![]() in der Regel ein Druckgradient ist. Im
Gegensatz zur Relaxationsrate des elektrischen Stroms gilt
in der Regel ein Druckgradient ist. Im
Gegensatz zur Relaxationsrate des elektrischen Stroms gilt ![]() , da weder
Phononen noch Fehlstellen existieren und Zweiteilchenstösse wegen des Fehlens
von Umklappprozessen nicht zur Impulsrelaxation führen. Die Relaxation ist
deshalb diffusiv und durch die Scherviskosität
, da weder
Phononen noch Fehlstellen existieren und Zweiteilchenstösse wegen des Fehlens
von Umklappprozessen nicht zur Impulsrelaxation führen. Die Relaxation ist
deshalb diffusiv und durch die Scherviskosität ![]() (Viskosität) bestimmt. Diese vermittelt auch den
Zusammenhang zwischen dem querschnittsgemittelten Massenstrom
(Viskosität) bestimmt. Diese vermittelt auch den
Zusammenhang zwischen dem querschnittsgemittelten Massenstrom ![]() der Flüssigkeit und dem von aussen angelegten
Druckgefälle, der als Hagen-Poiseuillesches Gesetz bekannt ist. Für Strömung
zwischen parallelen Platten (Abstand
der Flüssigkeit und dem von aussen angelegten
Druckgefälle, der als Hagen-Poiseuillesches Gesetz bekannt ist. Für Strömung
zwischen parallelen Platten (Abstand ![]() ) gilt
) gilt
![]()
Der Strömungswiderstand
![]() ist somit proportional zur Scherviskosität der
Flüssigkeit. Seine Beobachtbarkeit zu tieferen Temperaturen hin wird verdeckt
durch die in fast allen Fällen eintretende Verfestigung dieser Systeme. Nur
Flüssigkeiten, die aus besonders leichten Atomen (wie zum Beispiel die Isotope
des Heliums 4He
und 3He)
bestehen, bleiben bis zum absoluten Temperaturnullpunkt bei Atmosphärendruck
flüssig. Man nennt diese Systeme Quantenflüssigkeiten, da ihr flüssiger Zustand
durch die quantenmechanischen Nullpunktsbewegungen hervorgerufen wird.
ist somit proportional zur Scherviskosität der
Flüssigkeit. Seine Beobachtbarkeit zu tieferen Temperaturen hin wird verdeckt
durch die in fast allen Fällen eintretende Verfestigung dieser Systeme. Nur
Flüssigkeiten, die aus besonders leichten Atomen (wie zum Beispiel die Isotope
des Heliums 4He
und 3He)
bestehen, bleiben bis zum absoluten Temperaturnullpunkt bei Atmosphärendruck
flüssig. Man nennt diese Systeme Quantenflüssigkeiten, da ihr flüssiger Zustand
durch die quantenmechanischen Nullpunktsbewegungen hervorgerufen wird.
Im Jahre 1971
entdeckten David Lee, Douglas Osheroff und Robert Richardson bei einer
Sprungtemperatur ![]() von etwa zwei Tausendstel K den Übergang von
flüssigem 3He
in zwei superfluide Phasen. Obwohl im Gegensatz zur Impulsrelaxation die
Scherviskosität scheinbar verschwindet, wies ihr Verhalten sehr viele Analogien
zur Supraleitfähigkeit der »Elektronenflüssigkeit« in Metallen auf, zeigte
zusätzlich aber eine Vielzahl neuer und exotischer Eigenschaften. Diese
Entdeckung löste eine wahre Flut von experimentellen und theoretischen
Veröffentlichungen aus, die über mehr als zwei Dekaden anhielt und schliesslich
im Jahr 1996 mit dem Physik-Nobelpreis für die drei Entdecker ihre Würdigung
fand.
von etwa zwei Tausendstel K den Übergang von
flüssigem 3He
in zwei superfluide Phasen. Obwohl im Gegensatz zur Impulsrelaxation die
Scherviskosität scheinbar verschwindet, wies ihr Verhalten sehr viele Analogien
zur Supraleitfähigkeit der »Elektronenflüssigkeit« in Metallen auf, zeigte
zusätzlich aber eine Vielzahl neuer und exotischer Eigenschaften. Diese
Entdeckung löste eine wahre Flut von experimentellen und theoretischen
Veröffentlichungen aus, die über mehr als zwei Dekaden anhielt und schliesslich
im Jahr 1996 mit dem Physik-Nobelpreis für die drei Entdecker ihre Würdigung
fand.
Auch für neutrale
suprafluide Fermi-Systeme mit Teilchen der Masse ![]() und der superfluiden Dichte
und der superfluiden Dichte ![]() lässt sich die London-Theorie anwenden. Wegen
der fehlenden Ladung ist der supraleitende Massenstrom jetzt allein mit der
räumlichen Änderung der Phase der Kondensat-Wellenfunktion verknüpft:
lässt sich die London-Theorie anwenden. Wegen
der fehlenden Ladung ist der supraleitende Massenstrom jetzt allein mit der
räumlichen Änderung der Phase der Kondensat-Wellenfunktion verknüpft:
![]()
Die wesentliche
Gemeinsamkeit der Phänomene Supraleitung und Suprafluidität lässt sich nur mit
den Denkmethoden der Quantenmechanik verstehen. Sie besteht darin, dass es sich
bei Elektronen und 3He-Atomen,
welche Vielteilchensysteme von typischerweise 1023 Teilchen bilden, um Fermionen handelt,
d.h. Teilchen mit einem halbzahligen Spin. Fermionen gehorchen dem
Pauli-Prinzip, welches besagt, dass nur ein Fermion einen gegebenen
Quantenzustand ![]() ,
charakterisiert durch den Impuls
,
charakterisiert durch den Impuls ![]() und die Spinprojektion
und die Spinprojektion ![]() , besetzen kann.
(Bei flüssigem 4He
handelt es sich um ein Bosonen-System.)
, besetzen kann.
(Bei flüssigem 4He
handelt es sich um ein Bosonen-System.)
Ein moderner Zugang zu den Phänomenen Supraleitung (geladene Fermionen, Elektronen) und Suprafluidität (neutrale Fermionen) sollte diese auf ein und derselben Stufe behandeln. Ein erster Schritt in diese Richtung liess sehr lange, nämlich bis zum Jahre 1957, auf sich warten. In diesem Jahr veröffentlichten die Theoretiker John Bardeen, Leon Cooper und Robert Schrieffer (BCS) ihre mikroskopische Theorie der Supraleitung, nicht ahnend, dass sich diese Theorie, nach einigen nicht unwesentlichen Modifikationen, die insbesondere dem Theoretiker Anthony J. Leggett zu verdanken sind, auch zur Beschreibung der Suprafluidität von flüssigem 3He eignen würde. Wegen ihrer universellen Anwendbarkeit wurde die BCS-Theorie im Jahre 1972 mit dem Physik-Nobelpreis gewürdigt.
2 Klassifizierung paarkorrelierter Fermi-Systeme
Fermi-Systeme lassen
sich durch ihre Teilchendichte ![]() , mit
, mit ![]() der Fermi-Energie, das Energiespektrum
der Fermi-Energie, das Energiespektrum ![]() , mit
, mit ![]() dem chemischen Potential (
dem chemischen Potential (![]() ), die
Gruppengeschwindigkeit
), die
Gruppengeschwindigkeit ![]() und die Zustandsdichte an der Fermi-Kante
und die Zustandsdichte an der Fermi-Kante ![]() charakterisieren. Im globalen
thermodynamischen Gleichgewicht wird die mittlere Besetzungswahrscheinlichkeit
dieser Zustände durch die Impulsverteilung
charakterisieren. Im globalen
thermodynamischen Gleichgewicht wird die mittlere Besetzungswahrscheinlichkeit
dieser Zustände durch die Impulsverteilung
![]()
beschrieben. Hier
bedeuten ![]() und
und ![]() die Erzeugungs- und Vernichtungsoperatoren für
ein Fermion im Quantenzustand
die Erzeugungs- und Vernichtungsoperatoren für
ein Fermion im Quantenzustand ![]() und
und ![]() der statistische Mittelwert. Im Normalzustand
des Fermi-Systems ist
der statistische Mittelwert. Im Normalzustand
des Fermi-Systems ist ![]() die Fermi-Dirac-Verteilung
(Fermi-Dirac-Statistik).
die Fermi-Dirac-Verteilung
(Fermi-Dirac-Statistik).
Das BCS-Modell
postuliert, dass es bei tiefen Temperaturen energetisch günstiger ist, wenn sich
ein temperaturabhängiger Teil der Fermionen zu sog. Cooper-Paaren formiert. Der
geniale Aspekt an der Paarungshypothese ist die Einsicht, dass die Paarung nicht
im Orts- sondern im Impulsraum stattfindet. So ist die zentrale Annahme der
BCS-Theorie die spontane Paarformation im ![]() -Raum,
beschrieben durch einen im thermodynamischen Gleichgewicht endlichen
statistischen Mittelwert, die Paaramplitude
-Raum,
beschrieben durch einen im thermodynamischen Gleichgewicht endlichen
statistischen Mittelwert, die Paaramplitude
![]()
Hier ist ![]() der Relativimpuls des Paares. Das
Pauli-Prinzip erzwingt die totale Antisymmetrie von
der Relativimpuls des Paares. Das
Pauli-Prinzip erzwingt die totale Antisymmetrie von ![]() beim Vertauschen der Spins
beim Vertauschen der Spins ![]() ,
, ![]() und der Impulse
und der Impulse ![]() ,
, ![]() :
:
![]()
Die Spinabhängigkeit
der Paaramplitude wird durch die Möglichkeiten, zwei Spins vom Betrag ![]() und mit den Projektionen
und mit den Projektionen ![]() zum Gesamtspin
zum Gesamtspin ![]() und der Gesamtprojektion
und der Gesamtprojektion ![]() zu koppeln, festgelegt. Der
Clebsch-Gordon-Koeffizient für diese Kopplung lautet
zu koppeln, festgelegt. Der
Clebsch-Gordon-Koeffizient für diese Kopplung lautet
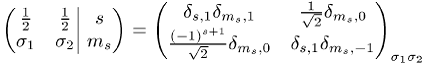
und lässt nur die
beiden Fälle ![]() (Singulett-Paarung) und
(Singulett-Paarung) und ![]() (Triplett-Paarung) zu. Für Singulett-Paarung
gilt
(Triplett-Paarung) zu. Für Singulett-Paarung
gilt
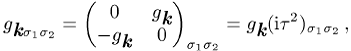
wobei ![]() . Hier ist
. Hier ist ![]() eine der Pauli-Matrizen, die zusammen mit der
Einheitsmatrix
eine der Pauli-Matrizen, die zusammen mit der
Einheitsmatrix ![]() ein vollständiges Basissystem von
ein vollständiges Basissystem von ![]() -Matrizen
bilden.
-Matrizen
bilden.
Wegen Gl. (7) muss ![]() für Singulett-Paarung gerade Parität bezüglich
für Singulett-Paarung gerade Parität bezüglich
![]() haben,
haben, ![]() . Die
. Die ![]() -Abhängigkeit
von
-Abhängigkeit
von ![]() lässt sich mit einer orbitalen Quantenzahl
lässt sich mit einer orbitalen Quantenzahl ![]() klassifizieren, und man spricht von
s-Wellen-Paarung (
klassifizieren, und man spricht von
s-Wellen-Paarung (![]() ),
d-Wellen-Paarung (
),
d-Wellen-Paarung (![]() ) usw. Im Fall
der Spin-Triplett-Paarung hat man
) usw. Im Fall
der Spin-Triplett-Paarung hat man
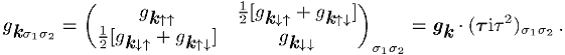
Die
Triplett-Komponenten ![]() ,
, ![]() , und
, und ![]() des Paaramplituden-Vektors
des Paaramplituden-Vektors ![]() sind den magnetischen Quantenzahlen
sind den magnetischen Quantenzahlen ![]() zugeordnet und haben wegen (7) ungerade
Parität bezüglich
zugeordnet und haben wegen (7) ungerade
Parität bezüglich ![]() ,
, ![]() . Im Fall der
Triplett-Paarung ist die orbitale Quantenzahl
. Im Fall der
Triplett-Paarung ist die orbitale Quantenzahl ![]() ungerade und man spricht von p-Wellen-Paarung
(
ungerade und man spricht von p-Wellen-Paarung
(![]() ),
f-Wellen-Paarung (
),
f-Wellen-Paarung (![]() ) u.s.w. Man
erkennt, dass mit dem supraleitenden Phasenübergang eine spontan gebrochene
Symmetrie verknüpft ist, nämlich die bezüglich der lokalen Eichtransformation
) u.s.w. Man
erkennt, dass mit dem supraleitenden Phasenübergang eine spontan gebrochene
Symmetrie verknüpft ist, nämlich die bezüglich der lokalen Eichtransformation ![]() , bei der die
Paaramplitude
, bei der die
Paaramplitude ![]() in
in ![]() übergeht (spontane Symmetriebrechung). Die
Formation von Cooper-Paaren wird durch eine in der Nähe der Fermi-Kante
anziehende Wechselwirkung
übergeht (spontane Symmetriebrechung). Die
Formation von Cooper-Paaren wird durch eine in der Nähe der Fermi-Kante
anziehende Wechselwirkung ![]() vermittelt, welche die mittleren
Paaramplituden
vermittelt, welche die mittleren
Paaramplituden ![]() und
und ![]() mit einer neuen Energieskala, dem mittleren
sog. Paarpotential verknüpft:
mit einer neuen Energieskala, dem mittleren
sog. Paarpotential verknüpft:
![]()
Die skalaren und
vektoriellen Paaramplituden ![]() ,
, ![]() , oder
äquivalent dazu, die Paarpotentiale
, oder
äquivalent dazu, die Paarpotentiale ![]() und
und ![]() , werden auch
als Ordnungsparameter (Phasenübergänge) der supraleitenden oder superfluiden
Phase des paarkorrelierten Fermi-Systems bezeichnet. Die Cooper-Paare, deren
Gesamtheit man auch als Kondensat bezeichnet, bilden nun den neuartigen
kollektiven Zustand makroskopischer Quantenkohärenz, der bereits in der
London-Theorie antizipiert worden ist. Durch die Paarungshypothese liefert die
BCS-Leggett-Theorie im Gegensatz zur London-Theorie nicht nur den korrekten
Wert für das im Doll-Näbauer-Experiment bestimmte Flussquantum, sondern erlaubt
auch eine korrekte Beschreibung der thermodynamischen, elektromagnetischen,
hydrodynamischen und spindynamischen Eigenschaften supraleitender und
superfluider Fermi-Systeme.
, werden auch
als Ordnungsparameter (Phasenübergänge) der supraleitenden oder superfluiden
Phase des paarkorrelierten Fermi-Systems bezeichnet. Die Cooper-Paare, deren
Gesamtheit man auch als Kondensat bezeichnet, bilden nun den neuartigen
kollektiven Zustand makroskopischer Quantenkohärenz, der bereits in der
London-Theorie antizipiert worden ist. Durch die Paarungshypothese liefert die
BCS-Leggett-Theorie im Gegensatz zur London-Theorie nicht nur den korrekten
Wert für das im Doll-Näbauer-Experiment bestimmte Flussquantum, sondern erlaubt
auch eine korrekte Beschreibung der thermodynamischen, elektromagnetischen,
hydrodynamischen und spindynamischen Eigenschaften supraleitender und
superfluider Fermi-Systeme.
Im folgenden sollen nun einige der in der Natur vorkommenden paarkorrelierten Fermi-Systeme durch die Form ihrer Paarpotentiale charakterisiert werden. Hierzu zerlegen wir
![]()
in den
temperaturabhängigen Maximalwert ![]() und einen
und einen ![]() -abhängigen
orbitalen Anteil, der die Möglichkeit einer Anisotropie auf der Fermi-Fläche
enthält. Man kann in unterschiedlichen Fermi-Systemen die Symmetrie des
Paarpotentials mit der der Fermi-Fläche bzw. der Bandstruktur vergleichen. Sind
diese Symmetrien gleich (oder ist nur die Eichsymmetrie spontan gebrochen), so
wird die Paarung als konventionell (k) bezeichnet. Ist die Symmetrie des
Paarpotentials geringer als die der Fermi-Fläche (oder gibt es neben der
Eichsymmetrie noch zusätzliche spontan gebrochene Symmetrien), so nennt man die
Paarung unkonventionell (u).
-abhängigen
orbitalen Anteil, der die Möglichkeit einer Anisotropie auf der Fermi-Fläche
enthält. Man kann in unterschiedlichen Fermi-Systemen die Symmetrie des
Paarpotentials mit der der Fermi-Fläche bzw. der Bandstruktur vergleichen. Sind
diese Symmetrien gleich (oder ist nur die Eichsymmetrie spontan gebrochen), so
wird die Paarung als konventionell (k) bezeichnet. Ist die Symmetrie des
Paarpotentials geringer als die der Fermi-Fläche (oder gibt es neben der
Eichsymmetrie noch zusätzliche spontan gebrochene Symmetrien), so nennt man die
Paarung unkonventionell (u).
In die siebziger und
achtziger Jahre fiel die Entdeckung neuer, exotischer Supraleiter. Dazu gehören
organische Supraleiter und Supraleiter mit sog. schweren Fermionen. Im Jahre
1986 wurden Materialien auf Kupferoxidbasis (Kuprate) mit Sprungtemperaturen
bis zu 153 K (sog. Hochtemperatur-Supraleiter) durch Karl Alex Müller und Georg
Bednorz entdeckt, die dafür im Jahr darauf mit dem Nobelpreis für Physik geehrt
wurden. Man ist heute davon überzeugt, dass die superfluiden Phasen des 3He, u.a. der
Schwerfermionsupraleiter UPt3,
sowie alle lochdotierten (ld) Kuprat-Supraleiter einen unkonventionellen
Ordnungsparameter haben. Unerwarteterweise zeigen die elektrondotierten (ed)
Kuprate scheinbar konventionelles Verhalten. Eine spezielle Konsequenz dieser
Unkonventionalität ist die Tatsache, dass der Ordnungsparameter Nulldurchgänge oder
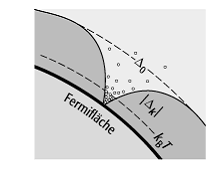
Noden haben kann, d.h. er kann auf der Fermi-Fläche Punkt- (P) oder Linien- (L)
förmige Nullstellen haben. Dieser Sachverhalt ist in [40]Abb. 1 veranschaulicht. In Tab. 1 sind
die Eigenschaften einiger wichtiger supraleitender (SL) und superfluider
Fermi-Systeme zusammengestellt. Die Fermi-Flächen werden der Einfachheit halber
als sphärisch (D = 3) oder als zylindrisch (D = 2) angenommen. Aufgeführt sind
Ordnungsparametersymmetrie, Nodenstruktur und die Dimensionalität D ihrer Fermi-Fläche.
In Tab. 1 ist ![]() der (Polar-) Winkel zwischen einer für den
Paarzustand charakteristischen makroskopischen orbitalen Vorzugsrichtung
der (Polar-) Winkel zwischen einer für den
Paarzustand charakteristischen makroskopischen orbitalen Vorzugsrichtung ![]() und dem Einheitsvektor
und dem Einheitsvektor ![]() auf der Fermi-Fläche. Für den Fall der
Triplett-Paarung ist
auf der Fermi-Fläche. Für den Fall der
Triplett-Paarung ist ![]() eine makroskopische Vorzugsrichtung im
Spinraum.
eine makroskopische Vorzugsrichtung im
Spinraum. ![]() ist eine Rotationsmatrix, welche im
Spezialfall des pseudoisotropen Zustands die Korrelation zwischen Spin- und
Bahnfreiheitsgraden der Cooper-Paare beschreibt. Der Winkel
ist eine Rotationsmatrix, welche im
Spezialfall des pseudoisotropen Zustands die Korrelation zwischen Spin- und
Bahnfreiheitsgraden der Cooper-Paare beschreibt. Der Winkel ![]() spielt dabei die gleiche Rolle wie der Winkel
zwischen
spielt dabei die gleiche Rolle wie der Winkel
zwischen ![]() und
und ![]() und reflektiert eine von Leggett erstmals
diskutierte zusätzliche spontan gebrochene Symmetrie, nämlich die relative
Spin-Bahn-Symmetrie des superfluiden Fermi-Systems (und damit den
unkonventionellen Charakter des Ordnungsparameters). Da es sich bei den
Kupraten um Quasi-2-
und reflektiert eine von Leggett erstmals
diskutierte zusätzliche spontan gebrochene Symmetrie, nämlich die relative
Spin-Bahn-Symmetrie des superfluiden Fermi-Systems (und damit den
unkonventionellen Charakter des Ordnungsparameters). Da es sich bei den
Kupraten um Quasi-2-![]() -Systeme
handelt, wird die
-Systeme
handelt, wird die ![]() -Symmetrie des
Paarpotentials durch den (Azimuth-) Winkel
-Symmetrie des
Paarpotentials durch den (Azimuth-) Winkel ![]() beschrieben.
beschrieben.
3 Paarkorrelierte Fermi-Systeme im thermischen Gleichgewicht
In der BCS-Behandlung
werden die Paarwechselwirkungseffekte durch einen Hamilton-Operator in
Molekularfeldnäherung erfasst. Die folgende Diskussion wird nun der
Übersichtlichkeit wegen auf den Fall der Singulett-Paarung beschränkt. Die
Resultate lassen sich jedoch problemlos auf den Triplett-Fall verallgemeinern.
Kombiniert man fermionische Erzeugungs- und Vernichtungsoperatoren zu einer
zweikomponentigen Grösse, einem sog. Spinor ![]() , dann ist
dieser Hamilton-Operator formal dem des Normalzustands äquivalent
(Nambu-Formalismus),
, dann ist
dieser Hamilton-Operator formal dem des Normalzustands äquivalent
(Nambu-Formalismus),
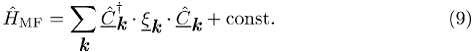
Hier ist ![]() jedoch eine Energiematrix
jedoch eine Energiematrix
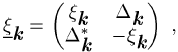
in deren Diagonale die
typischen Energien für teilchenartige (![]() ) und
lochartige (
) und
lochartige (![]() ) Anregungen
stehen. Das mittlere Paarpotential bildet die Nebendiagonalelemente und führt
zu einer Mischung von Teilchen- und Lochbeiträgen zur Energie. Wegen der
spontanen Paarformation
) Anregungen
stehen. Das mittlere Paarpotential bildet die Nebendiagonalelemente und führt
zu einer Mischung von Teilchen- und Lochbeiträgen zur Energie. Wegen der
spontanen Paarformation ![]() für
für ![]() spricht man im Zusammenhang mit dem Phänomen
der Supraleitung und der Suprafluidität auch von nebendiagonaler
langreichweitiger Ordnung.
spricht man im Zusammenhang mit dem Phänomen
der Supraleitung und der Suprafluidität auch von nebendiagonaler
langreichweitiger Ordnung.
Der Hamilton-Operator bzw. die Energiematrix werden diagonalisiert durch die Bogoljubow-Walatin-Transformation
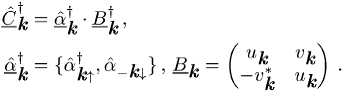
Da die neuen
Erzeugungs- und Vernichtungsoperatoren wieder fermionische Anregungen
beschreiben, gilt ![]() . Man erhält
. Man erhält
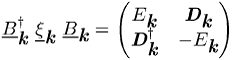
Die Bedingung ![]() legt die Amplituden
legt die Amplituden ![]() und
und ![]() fest:
fest: ![]() ,
, ![]() wobei
wobei
![]()
Die physikalische
Bedeutung von ![]() erkennt man aus der Form des transformierten
Hamilton-Operators
erkennt man aus der Form des transformierten
Hamilton-Operators
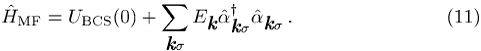
Der erste Term in (11)
ist die Gesamtenergie des BCS-Grundzustands, während der zweite Term den
Beitrag der thermischen Anregungen, der sog. Bogoljubow-Quasiteilchen bei
endlichen Temperaturen beschreibt. ![]() ist somit das Energiespektrum der
Bogoljubow-Quasiteilchen. Das Paarpotential
ist somit das Energiespektrum der
Bogoljubow-Quasiteilchen. Das Paarpotential ![]() spielt damit die Rolle einer im allgemeinen
anisotropen Energielücke im Spektrum der thermischen Anregungen. Die
thermischen Eigenschaften der Bogoljubow-Quasiteilchen werden durch die
Verteilungsfunktion
spielt damit die Rolle einer im allgemeinen
anisotropen Energielücke im Spektrum der thermischen Anregungen. Die
thermischen Eigenschaften der Bogoljubow-Quasiteilchen werden durch die
Verteilungsfunktion
![]()
und ihre Ableitung
nach ![]() ,
, ![]() beschrieben. Im globalen thermodynamischen
Gleichgewicht ergibt sich die diagonale Verteilungsfunktion
beschrieben. Im globalen thermodynamischen
Gleichgewicht ergibt sich die diagonale Verteilungsfunktion ![]() (vgl. (5)) nach der Bogoljubow-Walatin-Transformation
zu
(vgl. (5)) nach der Bogoljubow-Walatin-Transformation
zu
![]()
Es ist bemerkenswert,
dass die Ableitung von ![]() ,
, ![]() , bei allen
Temperaturen
, bei allen
Temperaturen ![]() der Summenregel
der Summenregel ![]() genügt.
genügt.
Die Gleichgewichts-Paaramplitude (vgl. (7)) lautet nach der Bogoljubow-Walatin-Transformation
![]()
Die Ursachen und
Mechanismen für die Paaranziehung ![]() sind unterschiedlich. Bei konventionellen
Supraleitern vermitteln meistens die Quanten der Gitterschwingungen, die
Phononen, eine Paaranziehung zwischen den Elektronen. In einigen Klassen
unkonventioneller Supraleiter (Schwerfermion-, Hochtemperatur-Supraleiter sowie
die superfluide Fermi-Flüssigkeit 3He) glaubt man heute, dass antiferromagnetische bzw.
ferromagnetische sog. Spinfluktuationen oder Paramagnonen die Paaranziehung
verursachen. Wir müssen an dieser Stelle auf eine Diskusion der mikroskopischen
Ursachen für die Paarattraktion verzichten und nehmen lediglich an, dass die
Paarwechselwirkung sehr klein (
sind unterschiedlich. Bei konventionellen
Supraleitern vermitteln meistens die Quanten der Gitterschwingungen, die
Phononen, eine Paaranziehung zwischen den Elektronen. In einigen Klassen
unkonventioneller Supraleiter (Schwerfermion-, Hochtemperatur-Supraleiter sowie
die superfluide Fermi-Flüssigkeit 3He) glaubt man heute, dass antiferromagnetische bzw.
ferromagnetische sog. Spinfluktuationen oder Paramagnonen die Paaranziehung
verursachen. Wir müssen an dieser Stelle auf eine Diskusion der mikroskopischen
Ursachen für die Paarattraktion verzichten und nehmen lediglich an, dass die
Paarwechselwirkung sehr klein (![]() ) wegen
dieser Annahme spricht man im Zusammenhang mit Supraleitung und Suprafluidität
auch vom Limes schwacher Kopplung und in einer Energieschale der Dicke
) wegen
dieser Annahme spricht man im Zusammenhang mit Supraleitung und Suprafluidität
auch vom Limes schwacher Kopplung und in einer Energieschale der Dicke ![]() um die Fermi-Energie anziehend ist. Die Lösung
der Energielückengleichung (8) bei endlichen Temperaturen geschieht durch
Einsetzen der Paaramplitude (14) in Gl. (8) und liefert bei der
Sprungtemperatur und bei
um die Fermi-Energie anziehend ist. Die Lösung
der Energielückengleichung (8) bei endlichen Temperaturen geschieht durch
Einsetzen der Paaramplitude (14) in Gl. (8) und liefert bei der
Sprungtemperatur und bei ![]() die beiden im Limes schwacher Kopplung
universellen sog. BCS-Mühlschlegel-Parameter, nämlich den für die
Molekularfeldnäherung typischen Sprung in der spezifischen Wärme bei
die beiden im Limes schwacher Kopplung
universellen sog. BCS-Mühlschlegel-Parameter, nämlich den für die
Molekularfeldnäherung typischen Sprung in der spezifischen Wärme bei ![]() und die Energielücke bei
und die Energielücke bei ![]() :
:
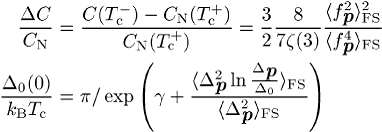
Hier ist ![]() die Eulersche Konstante,
die Eulersche Konstante, ![]() die Riemannsche
die Riemannsche ![]() -Funktion;
-Funktion; ![]() bedeutet eine Mittelung über die Fermi-Fläche
und
bedeutet eine Mittelung über die Fermi-Fläche
und ![]() ist die Wärmekapazität des normalen
Fermi-Systems. In Tabelle 2 findet man eine Zusammenstellung von
BCS-Mühlschlegel-Parametern für einige repräsentative paarkorrelierte
Fermi-Systeme. Für Temperaturen
ist die Wärmekapazität des normalen
Fermi-Systems. In Tabelle 2 findet man eine Zusammenstellung von
BCS-Mühlschlegel-Parametern für einige repräsentative paarkorrelierte
Fermi-Systeme. Für Temperaturen ![]() lässt sich die maximale Energielücke wie folgt
interpolieren:
lässt sich die maximale Energielücke wie folgt
interpolieren:
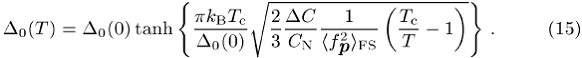
4 Paarkorrelierte Fermi-Systeme in äusseren Feldern
Schliesslich
untersuchen wir, wie supraleitende und superfluide Fermi-Systeme auf die
Gegenwart räumlich und zeitlich schwach veränderlicher äusserer Störungen wie
ein Vektorpotential ![]() , ein
Magnetfeld
, ein
Magnetfeld ![]() oder eine lokale Temperaturänderung
oder eine lokale Temperaturänderung ![]() bei beliebigen Temperaturen
bei beliebigen Temperaturen ![]() reagieren. Eine solche Situation lässt sich
besonders einfach durch die Annahme des sog. lokalen Gleichgewichts
beschreiben. Das bedeutet, dass die Impulsverteilung
reagieren. Eine solche Situation lässt sich
besonders einfach durch die Annahme des sog. lokalen Gleichgewichts
beschreiben. Das bedeutet, dass die Impulsverteilung ![]() der Bogoljubow-Quasiteilchen auch in Gegenwart
der Störungen noch eine Fermi-Funktion
der Bogoljubow-Quasiteilchen auch in Gegenwart
der Störungen noch eine Fermi-Funktion ![]() ist,
ist,
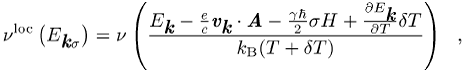
in der aber das
Argument von ![]() nach
nach ![]() verschoben ist, wobei
verschoben ist, wobei ![]() und
und ![]() das gyromagnetische Verhältnis der Fermionen
ist. Die lokale lineare Antwort (linear response) des gesamten
Quasiteilchensystems führt bei einer Temperaturänderung
das gyromagnetische Verhältnis der Fermionen
ist. Die lokale lineare Antwort (linear response) des gesamten
Quasiteilchensystems führt bei einer Temperaturänderung ![]() auf die Entropieänderung
auf die Entropieänderung ![]() , beim Anlegen
eines Magnetfeldes
, beim Anlegen
eines Magnetfeldes ![]() auf die Spinmagnetisierung
auf die Spinmagnetisierung ![]() und bei Anwesenheit des Vektorpotentials
und bei Anwesenheit des Vektorpotentials ![]() auf den elektronischen Quasiteilchenstrom
auf den elektronischen Quasiteilchenstrom ![]() . Die
entsprechenden sog. Responsefunktionen sind die Wärmekapazität
. Die
entsprechenden sog. Responsefunktionen sind die Wärmekapazität ![]() , die Paulische
Spinsuszeptibilität
, die Paulische
Spinsuszeptibilität ![]() und der Stromresponse-Tensor
und der Stromresponse-Tensor ![]() . Im folgenden
fassen wir die Resultate für diese Grössen bei beliebigen Temperaturen zusammen
(bei den numerischen Rechnungen wurde die Interpolationsformel (15) für
. Im folgenden
fassen wir die Resultate für diese Grössen bei beliebigen Temperaturen zusammen
(bei den numerischen Rechnungen wurde die Interpolationsformel (15) für ![]() verwendet):
verwendet):
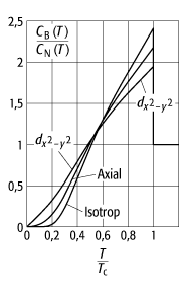
1. Wärmekapazität der Bogoljubow-Quasiteilchen:
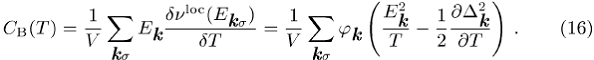
[41]Abb. 2 zeigt die
Temperaturabhängigkeit der normierten Wärmekapazität ![]() für einige paarkorrelierte Fermi-Systeme. Die
Resultate für den
für einige paarkorrelierte Fermi-Systeme. Die
Resultate für den ![]() - und
- und ![]() -Zustand liegen
sehr nahe an der Kurve für
-Zustand liegen
sehr nahe an der Kurve für ![]() -Paarung und
sind daher nicht eingezeichnet. Man beachte, dass mit zunehmender
Energielückenanisotropie die Diskontinuität in
-Paarung und
sind daher nicht eingezeichnet. Man beachte, dass mit zunehmender
Energielückenanisotropie die Diskontinuität in ![]() bei
bei ![]() in demselben Masse abnimmt wie der Anstieg von
in demselben Masse abnimmt wie der Anstieg von ![]() bei tiefen Temperaturen zunimmt
(Entropie-Summenregel).
bei tiefen Temperaturen zunimmt
(Entropie-Summenregel).
2. Spinsuszeptibilität
der Bogoljubow-Quasiteilchen: 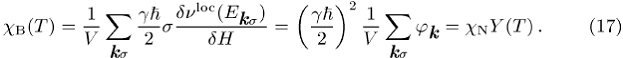
Hier ist ![]() die Paulische Spinsuszeptibilität des
Normalzustands. Die Temperaturabhängigkeit der Spinsuszeptibilität wird durch
die dimensionslose sog. Yosida-Funktion
die Paulische Spinsuszeptibilität des
Normalzustands. Die Temperaturabhängigkeit der Spinsuszeptibilität wird durch
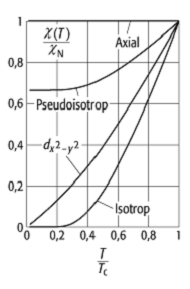
die dimensionslose sog. Yosida-Funktion ![]() beschrieben. [42]Abb. 3 zeigt die
Temperaturabhängigkeit der normierten Spinsuszeptibilität
beschrieben. [42]Abb. 3 zeigt die
Temperaturabhängigkeit der normierten Spinsuszeptibilität ![]() für einige paarkorrelierte Fermi-Systeme. Die
Resultate für den
für einige paarkorrelierte Fermi-Systeme. Die
Resultate für den ![]() - und
- und ![]() -Zustand liegen
sehr nahe an der Kurve für
-Zustand liegen
sehr nahe an der Kurve für ![]() -Paarung und sind
daher nicht eingezeichnet. Besonders deutlich wird der Unterschied zwischen dem
thermisch aktivierten konventionellen Verhalten und dem linearen
Tieftemperaturpotenzgesetz für die Energielücken mit Liniennoden. Bei der
Berechnung der Spinsuszeptibilität in Systemen mit Spin-Triplett-Paarung ist zu
beachten, dass sich die
-Paarung und sind
daher nicht eingezeichnet. Besonders deutlich wird der Unterschied zwischen dem
thermisch aktivierten konventionellen Verhalten und dem linearen
Tieftemperaturpotenzgesetz für die Energielücken mit Liniennoden. Bei der
Berechnung der Spinsuszeptibilität in Systemen mit Spin-Triplett-Paarung ist zu
beachten, dass sich die ![]() -Komponenten
des Tripletts paramagnetisch verhalten, d.h. sie tragen einen konstanten
(Pauli-) Beitrag zur Suszeptibilität bei. Die
-Komponenten
des Tripletts paramagnetisch verhalten, d.h. sie tragen einen konstanten
(Pauli-) Beitrag zur Suszeptibilität bei. Die ![]() -Komponente
repräsentiert den Beitrag der thermischen Anregungen und verschwindet im Limes
-Komponente
repräsentiert den Beitrag der thermischen Anregungen und verschwindet im Limes ![]() . So stellt die
temperaturabhängige Grösse
. So stellt die
temperaturabhängige Grösse ![]() im Fall von 3He-B nur den
im Fall von 3He-B nur den ![]() -Beitrag (
-Beitrag (![]() ) des
Spin-Tripletts dar. Mit den fehlenden
) des
Spin-Tripletts dar. Mit den fehlenden ![]() -Beiträgen (
-Beiträgen (![]() ) lautet die
gesamte Spinsuszeptibilität von 3He-B
) lautet die
gesamte Spinsuszeptibilität von 3He-B ![]() , wenn
Wechselwirkungseffekte vernachlässigt werden. Der axiale Zustand zur
Beschreibung von 3He-A besitzt im einfachsten Fall (
, wenn
Wechselwirkungseffekte vernachlässigt werden. Der axiale Zustand zur
Beschreibung von 3He-A besitzt im einfachsten Fall (![]() ) nur die
paramagnetischen
) nur die
paramagnetischen ![]() -Komponenten
des Spin-Tripletts (man spricht deshalb auch von »equal spin pairing«). Daher
behält die Spinsuszeptibilität bei allen Temperaturen
-Komponenten
des Spin-Tripletts (man spricht deshalb auch von »equal spin pairing«). Daher
behält die Spinsuszeptibilität bei allen Temperaturen ![]() ihren Normalzustands-(Pauli-)Wert. Für den
ihren Normalzustands-(Pauli-)Wert. Für den ![]() -Zustand gilt
im einfachsten Fall
-Zustand gilt
im einfachsten Fall ![]() . Somit trägt
nur die
. Somit trägt
nur die ![]() -Komponente des
Tripletts zur Spinsuszeptibilität bei,
-Komponente des
Tripletts zur Spinsuszeptibilität bei, ![]() .
.
3. Stromresponse der Bogoljubow-Quasiteilchen
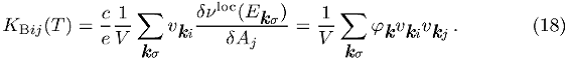
Die Grösse ![]() beschreibt den Quasiteilchenbeitrag zum
gesamten elektronischen Suprastrom
beschreibt den Quasiteilchenbeitrag zum
gesamten elektronischen Suprastrom ![]() , in dem
, in dem ![]() und
und ![]() der diamagnetische Anteil des Stroms ist. Man
beachte, dass das Vektorpotential durch einen Phasengradienten ergänzt worden
ist (Eichtransformation des Vektorpotentials
der diamagnetische Anteil des Stroms ist. Man
beachte, dass das Vektorpotential durch einen Phasengradienten ergänzt worden
ist (Eichtransformation des Vektorpotentials ![]() ), um dem
Resultat für den Suprastrom eine eichinvariante Form zu geben. Die Ersetzung
), um dem
Resultat für den Suprastrom eine eichinvariante Form zu geben. Die Ersetzung ![]() verknüpft
verknüpft ![]() mit der Variablen
mit der Variablen ![]() , welche die
gebrochene Eichsymmetrie beschreibt. Somit sind die eichinvarianten Ausdrücke
für den elektronischen Suprastrom
, welche die
gebrochene Eichsymmetrie beschreibt. Somit sind die eichinvarianten Ausdrücke
für den elektronischen Suprastrom
![]()
und den superfluiden Massenstrom aus der BCS-Theorie
![]()
formal identisch mit
den entsprechenden Resultaten (2) und (4) der London-Theorie, mit dem einzigen
Unterschied, dass man die Grösse ![]() im Rahmen der BCS-Theorie berechnen kann.
im Rahmen der BCS-Theorie berechnen kann.
Für den Fall einer
(uniaxialen) Anisotropie (Achse ![]() ) der
Fermi-Fläche (
) der
Fermi-Fläche (![]() , mit
, mit ![]() ,
, ![]() ,
, ![]() den Kristallachsen) oder der Energielücke (
den Kristallachsen) oder der Energielücke (![]() ) gilt
) gilt ![]() . Der
London-BCS-Strom, in die Maxwell-Gleichung
. Der
London-BCS-Strom, in die Maxwell-Gleichung ![]() eingesetzt, beschreibt die
Magnetfeldabschirmung des Supraleiters, charakterisiert durch die beiden
London-BCS-Eindringtiefen
eingesetzt, beschreibt die
Magnetfeldabschirmung des Supraleiters, charakterisiert durch die beiden
London-BCS-Eindringtiefen ![]() . Für isotrope Fermi-Systeme
ist
. Für isotrope Fermi-Systeme
ist ![]() mit der superfluiden Dichte
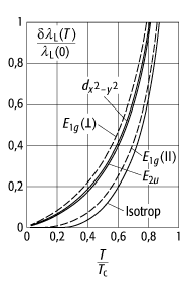
mit der superfluiden Dichte ![]() . In [43]Abb. 4 ist die Temperaturabhängigkeit
der normierten Magnetfeldeindringtiefe
. In [43]Abb. 4 ist die Temperaturabhängigkeit
der normierten Magnetfeldeindringtiefe ![]() für einige Supraleiter gezeigt. Der
Unterschied zwischen dem thermisch aktivierten Tieftemperaturverhalten für
isotrope Paarung und den linearen Tieftemperaturpotenzgesetzen für den Fall der
Dominanz von Liniennoden ist auch in dieser Grösse deutlich. Man beachte, dass
die
für einige Supraleiter gezeigt. Der
Unterschied zwischen dem thermisch aktivierten Tieftemperaturverhalten für
isotrope Paarung und den linearen Tieftemperaturpotenzgesetzen für den Fall der
Dominanz von Liniennoden ist auch in dieser Grösse deutlich. Man beachte, dass
die ![]() - im Gegensatz
zur
- im Gegensatz
zur ![]() -Energielücke
eine starke Anisotropie in den
-Energielücke
eine starke Anisotropie in den ![]() -Komponenten
aufweist. Dies könnte für die Identifikation der Ordnungsparametersymmetrie in
UPt3 nützlich sein.
-Komponenten
aufweist. Dies könnte für die Identifikation der Ordnungsparametersymmetrie in
UPt3 nützlich sein.
Das
Tieftemperaturverhalten der lokalen Responsefunktionen für isotrope
Energielücken ist thermisch aktiviert, ![]() und damit qualitativ unterschiedlich von dem
für Energielücken mit Nodenstruktur. Im letzteren Fall existieren thermische
Anregungen, in [44]Abb. 1 durch kleine Kreise
symbolisiert, bei tiefen Temperaturen
und damit qualitativ unterschiedlich von dem
für Energielücken mit Nodenstruktur. Im letzteren Fall existieren thermische
Anregungen, in [44]Abb. 1 durch kleine Kreise
symbolisiert, bei tiefen Temperaturen ![]() besonders in der Umgebung der Noden, was zu
den in Abbildungen 2-4 sichtbaren Potenzgesetzen für die Responsefunktionen
führt. In Tabelle 3 sind analytische Resultate für das Tieftemperaturverhalten
der drei oben abgeleiteten Responsefunktionen für einige supraleitende und
superfluide Systeme zusammengestellt.
besonders in der Umgebung der Noden, was zu
den in Abbildungen 2-4 sichtbaren Potenzgesetzen für die Responsefunktionen
führt. In Tabelle 3 sind analytische Resultate für das Tieftemperaturverhalten
der drei oben abgeleiteten Responsefunktionen für einige supraleitende und
superfluide Systeme zusammengestellt.
Experimentelle
Resultate sind im Fall der superfluiden Phasen des 3He, lochdotierter Kuprate und des
Schwerfermionsupraleiters UPt3 im Einklang mit der Annahme unkonventioneller
Cooper-Paarung. Während die Annahme von p-Wellen-Triplett-Paarung in 3He-A und -B zu einem
weitgehend quantitativen Verständnis von Thermodynamik, Transport, Spindynamik
und der kollektiven Moden geführt hat, lassen sich die lochdotierten Kuprate,
zumindest bei optimaler Dotierung, qualitativ auf der Basis von Singulett-![]() -Paarung
verstehen. Eine mögliche Dotierungsabhängigkeit der Paarsymmetrie ist
Gegenstand von gegenwärtigen Untersuchungen. Die Identifikation der Symmetrie
des Ordnungsparameters in UPt3 ist noch nicht endgültig gesichert, jedoch sind die
-Paarung
verstehen. Eine mögliche Dotierungsabhängigkeit der Paarsymmetrie ist
Gegenstand von gegenwärtigen Untersuchungen. Die Identifikation der Symmetrie
des Ordnungsparameters in UPt3 ist noch nicht endgültig gesichert, jedoch sind die ![]() - und
- und ![]() - Zustände
ernstzunehmende Kandidaten.
- Zustände
ernstzunehmende Kandidaten.
Zusammenfassend sei festgestellt, dass man die Eigenschaften einer grossen Klasse paarkorrelierter Fermi-Systeme im Gleichgewicht und in Gegenwart äusserer Felder im Rahmen einer erweiterten BCS-Theorie schwacher Kopplung verstehen kann. Das Postulat der Paarformation stellt hierbei den entscheidenden Aspekt der BCS-Theorie dar, unter dem sich die Phänomene der Supraleitung und der Suprafluidität vereinheitlichen lassen, wenn auch der Mechanismus, der zur Bildung der Cooper-Paare führt, in den verschiedenen Klassen supraleitender Systeme unterschiedlich sein kann.
Literatur:
M. Tinkham, Introduction to Superconductivity, McGraw Hill, 1996;
J. R. Waldram, Superconductivity of Metals and Cuprates, IOP Publishing Ltd, 1996;
J. B. Ketterson und S.N. Song, Superconductivity, Cambridge University Press, 1999;
P.G. deGennes, Superconductivity in Metals and Alloys, Perseus Books, 1999;
D. Vollhardt und P. Wölfle, The Superfluid Phases of Helium 3, Taylor & Francis, 1990;
T. Tsuneto, Superconductivity and Superfluidity, Cambridge University Press, 1998.
Supraleitung und Suprafluidität 1: Ordnungsparameter einiger Fermi-Systeme.
|
System |
Paarung |
|
Anisotropie |
Bezeichnung |
|
Noden |
|
Klass. SL |
|
k |
|
isotrop |
3 |
|
|
3He-A |
|
u |
|
axial |
3 |
P |
|
3He-B |
|
u |
|
pseudoisotrop |
3 |
|
|
UPt3 |
|
u |
|
|
3 |
P+L |
|
|
|
u |
|
|
3 |
P+L |
|
Kuprat-SL (l-d) |
|
u |
|
|
2 |
L |
|
Kuprat-SL (e-d) |
|
(?) |
|
(?) |
2 |
|
Supraleitung und Suprafluidität 2: BCS-Mühlschlegel-Parameter einiger Fermisysteme.
|
|
isotrop |
axial |
|
|
|
|
|
|
|
|
|
|
|
|
1,426 |
1,188 |
0,998 |
0,971 |
0,951 |
|
|
|
|
|
|
|
|
|
1,764 |
2,029 |
2,112 |
2,128 |
2,140 |
Supraleitung und Suprafluidität 3: Tieftemperaturverhalten einiger paarkorrelierter Fermi-Systeme.