Techniklexikon

Wackelschwingungen

Schwingungen und Wellen, nichtlineare Schwingungen mit charakteristischer Abhängigkeit der Frequenz von der Amplitude: Je kleiner die Amplitude wird, desto grösser wird die Frequenz. Daher ist bei erzwungenen Wackelschwingungen im Gegensatz zu den erzwungenen linearen Schwingungen kein Zerstören durch Resonanz möglich, solange die Erregerfrequenz eine untere Grenzfrequenz nicht unterschreitet.

Bekanntestes Beispiel für Wackelschwingungen dürften Münzen sein, die über den Tisch rollen. Der Amplitudenverlauf dieser Art von Schwingungen in Abhängigkeit von der Zeit ist schematisch in der Abbildung wiedergegeben.

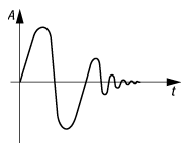
Wackelschwingungen: Amplitudenverlauf einer gedämpften Wackelschwingung mit der Zeit. Mit abnehmender Amplitude erhöht sich die Frequenz der Schwingung.