Techniklexikon

Resonanz

Jeder schwingungsfähige Körper und jedes schwingungsfähige System hat eine sog. Eigenfrequenz (Frequenz), die es nach einmaliger Anregung beibehält. Entspricht die anregende Frequenz der Eigenfrequenz, kommt es zu R. Dieser Effekt kann sehr störend wirken, aber auch genutzt werden, z. B. in der Hochfrequenztechnik zur Abstimmung von Sendern und Empfängern. Schwingungen und WellenAtom- und MolekülphysikAstronomie und Astrophysik, 1) Allgemein: Mitschwingen eines schwingungsfähigen physikalischen Systems, d.h. eines Resonators, bei Erregung durch eine äussere periodische Kraft, deren Frequenz w mit einer der Eigenfrequenzen (Resonanzfrequenzen) w₀ des Systems übereinstimmt oder in deren Nähe liegt (Schwingungen). Man spricht in diesem Fall von harmonischer Resonanz. Bei Erregung nichtlinearer Schwingungen tritt subharmonische Resonanz auf, wenn der Erreger mit der Frequenz , n, m ganze Zahlen, schwingt.

2) Atom- und Teilchenphysik: quasi-gebundener Zustand, der entsteht, wenn eine schwache Verbindung zwischen einem gebundenen und einem ungebundenen Zustand besteht. Resonanzen treten in Streuprozessen mit quantenmechanischem Charakter auf, man findet sie in vielen Bereichen der Physik, hauptsächlich in der Atom-, Kern- und Elementarteilchenphysik.

Die Verbindung zwischen gebundenem und ungebundenem Zustand kann durch zwei Mechanismen hergestellt werden, nach denen man Resonanzen unterscheidet:

1. Feshbach-Resonanz: Bei der Feshbach-Resonanz sind zwei separate Potentialkurven, die einen offenen und einen geschlossenen Streukanal darstellen, durch ein von Null verschiedenes Übergangsmatrixelement verbunden.

2. Shape-Resonanz: Die Shape-Resonanz wird durch die Form des eindimensionalen Wechselwirkungspotentials verursacht: Ein endlich hoher Potentialwall verbindet einen inneren Potentialtopf (der für sich alleine zur Bildung von gebundenen Zuständen führen würde) mit einem äusseren Potentialbereich, in dem klassisch nur ungebundene Zustände möglich sind. Eine solche Situation ist in Abb. (a) dargestellt. Die Potentialstruktur erlaubt zwei quasi-gebundene Zustände (Resonanzen).

Die Charakteristika einer Resonanz (sowohl Shape- als auch Feshbach-) sind in den Abb. (b) und (c) zu sehen: Bei den Resonanzenergien E₀ und E₁ steigt die Streuphase sprunghaft um einen Wert p an, was sich auch anhand der Lage der Knoten der Wellenfunktionen in (a) verfolgen lässt. Das Profil der Resonanzen (c) ist durch die Breit-Wigner-Formel beschrieben. Die Halbwertsbreite G der Peaks ist umgekehrt proportional zur Lebensdauer t der Resonanz: .

Die beiden Resonanzen in diesem Beispiel sind isolierte Resonanzen, da ihr Abstand grösser als die jeweilige Resonanzbreite ist. In der Realität sind die Charakteristika von Resonanzen nicht immer so ausgeprägt.

In hochenergetischen Streuprozessen der Teilchenphysik (z.B. Proton-Antiproton- oder Pion-Nukleon-Stösse) treten Resonanzen als Erhöhungen im Wirkungsquerschnitt auf. Ihre häufig sehr kurzen Lebensdauern deuten auf ihren Zerfall auf Grund der starken, z.T. auch der elektromagnetischen, Wechselwirkung hin. Man kann Resonanzen Massen zuordnen und ihre Quantenzahlen bestimmen; weitere Informationen erhält man aus der Analyse des Dalitz-Plots. Es treten sowohl baryonische Resonanzen (z.B. die D-Resonanz bei 1232 MeV), die im Quarkmodell der Baryonen als Anregungszustände der Quarktripletts klassifiziert werden, als auch mesonische Resonanzen (z.B. das r-Meson) auf (Elementarteilchen).

3) Astronomie: 1) ganzzahliges Verhältnis der Umlaufzeiten zweier Himmelskörper, die einen dritten umlaufen. Im Sonnensystem treten Resonanzen verschiedenster Art auf. Mit Resonanzen z.B. in den Umlaufperioden von Planetoiden und dem Planet Jupiter lassen sich Kommensurabilitätslücken erklären; 2) ganzzahliges Verhältnis der Umlaufzeit eines Himmelskörpers um einen anderen zu seiner Rotationsperiode. Dies ist z.B. bei der gebundenen Rotation des Mondes um die Erde der Fall.

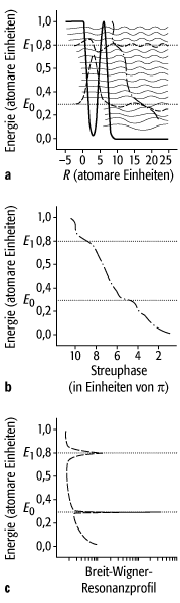
Resonanz: a) Wellenfunktionen im Potential  für , 1 für x < 0. Gestrichelte Linie: Resonanz-Wellenfunktion, strichpunktiert: Lage der Knoten der Wellenfunkionen; b) Streuphase als Funktion der Energie; c) Breit-Wigner-Resonanzprofil.