Alltagsphysik
Petra Nordinghaus-Martin
1. Einleitung
Was ist Alltagsphysik?
Wie fliegen Vögel, wie schwimmen Fische? Warum rauscht ein Bach? Wie rieselt Sand? Warum kennen wir nicht das Wetter von übermorgen? Warum hat die Erde ein magnetisches Feld?
Wann klebt Reis? Wie schmiert Öl? Wie entsteht Rost, wie verhindert man ihn? Ein Kind kann in wenigen Minuten mehr solcher Fragen stellen, als ein Nobelpreisträger in seinem ganzem Leben beantworten kann.
Diese Probleme haben mehrere Charakteristika gemeinsam, deren erstes und wichtigstes ist, dass wir sie in unserem alltäglichen Leben wahrnehmen können, ohne dazu mehr zu brauchen als wache Sinne oder einfache Beobachtungsmittel wie Stoppuhr, Lupe und Kompass. Die meisten solcher Fragestellungen haben ausserdem gemeinsam, dass sie offensichtlich naturwissenschaftlichen Charakter besitzen, aber nicht in die Abgrenzungen der herkömmlichen Disziplinen passen: Bei dem Erdmagnetfeld etwa spielen (mindestens) Mechanik der Drehbewegung, Strömungslehre, Elektrodynamik und Physik der kondensierten Materie zusammen, und ein Verständnis der bis heute nicht vollständig erklärten Kleb- und Schmiervorgänge ist nur durch intensive Zusammenarbeit von Physikern, Chemikern und Ingenieuren der Verfahrenstechnik möglich. Der Nobelpreis 1991 an Pierre-Gilles de Gennes wurde unter anderem für seine Beiträge zu einem theoretischen Verständnis von Grenzflächenvorgängen vergeben, und er selbst äussert trotz seiner eigenen Erfolge sehr deutlich die Begrenztheit unseres Wissens auf diesem Gebiet [1]. Ein Bereich, in dem de Gennes zur theoretischen Klärung hat beitragen können, sind Benetzungsphänomene [2], z.B. die Kontaktwinkelhysterese: Ein Flüssigkeitstropfen auf einer festen Unterlage nimmt keineswegs immer den durch die Energiebetrachtung festgelegten Randwinkel q0 der Young-Laplace-Gleichung an. Vielmehr kann der Randwinkel, wie sich bei dem Voranschreiten einer Regenspur am Fenster oder durch Neigen einer mit Wassertropfen besetzten Oberfläche leicht feststellen lässt, in einem weiten Bereich liegen:
wobei q ± der Randwinkel bei Vergrösserung bzw.
Verkleinerung der benetzten Oberfläche ist und cosq0 = sh/sg - fl mit der Haftspannung sh = sg - fe - sfl - fe (s:
Grenzflächenspannung; fe: feste, fl: flüssige, g: gasförmige Phase). Der Effekt
ist im wesentlichen auf die Rauhigkeit und/oder Verunreinigungen der festen
Oberfläche zurückzuführen und wird beschrieben durch die statistische Mechanik
der Wechselwirkung auf Zufallsflächen mit geometrischen oder chemischen
Defekten. Ein erstes interessantes Ergebnis ist, dass für kleine Störungen, also
unter der Voraussetzung 
<< 1, chemisches und geometrisches
Problem identisch werden, wenn man die Gleichsetzung
vornimmt, wobei Dsh die Schwankungen der Haftspannung um den Mittelwert aufgrund von Verunreinigungen und f(x) die Schwankungen des Oberflächenprofils aufgrund von Rauhigkeit bedeuten; x ist die Richtung senkrecht zur Kontaktlinie. Das Beispiel zeigt die Verbindung von einem zunächst banal erscheinenden Alltagsphänomen und anspruchsvoller Theorie, die auf dem Niveau des Gesamtwerkes von de Gennes schliesslich sogar des Nobelpreises würdig war.
Neben diesen Zusammenhängen mit offenen Fragen in der aktuellen Forschungsarbeit bieten viele Phänomene der Alltagsphysik auch die Möglichkeit, sich fundamentalen Fragestellungen der Physik in einer sehr anschaulichen Weise zu nähern. Als Beispiel hierfür können die bereits erwähnten Grenzflächenvorgänge gelten: Wer hätte noch nicht gesehen, wie sich Öl auf einer Wasseroberfläche verbreitet, und wer hätte nicht zumindest gehört, dass man so die Wogen glätten kann? Benjamin Franklin hat bereits um 1770 beobachtet, wie gross bei einem gegebenen Volumen Olivenöl ("a teaspoon", V » 2 cm3) die geglättete Wasseroberfläche ist ("half an acre", A » 2000 m2), und Lord Rayleigh hat 100 Jahre später hieraus auf die Existenz und die Dimensionen von kleinsten Bausteine der Materie geschlossen: Der Quotient V/A liefert die Dicke des Ölfilmes, nämlich etwa 10 Å - wie man heute weiss, gerade die Grössenordnung der Länge der Ölmoleküle! Hier versteht man, warum de Gennes die Alltagsphysik als Schule einer wissenschaftlichen Herangehensweise mit einfachsten Experimenten, einfachster Mathematik, aber viel Scharfsinn propagiert, einer Herangehensweise, der er auch nach obigem Musterbeispiel einen Namen gegeben hat: der "Franklinsche Geist" [1, S. 100ff]. Die andere Seite der Medaille, dass nämlich Alltagsphänomene (wie die Kontaktwinkelhysterese, s.o.) auch ausgesprochen anspruchsvolle Theorie erfordern können, sollte aber nicht vergessen werden.
Damit können wir nun
die in der Überschrift dieses Abschnittes gestellte Frage beantworten:
Alltägliche Beobachtungssituation und einfache Beobachtungsmittel sowie,
zumindest als Teilaspekt des fraglichen Phänomens, ein ausgeprägt
naturwissenschaftlicher (oft interdisziplinärer) Bezug machen die Definition
des Begriffes "Alltagsphysik" aus, wie er in diesem Lexikon aufgefasst
wird.
Klassifizierung der Alltagsphysik
Anhand der obigen Beispiele wird auch ein weiteres Charakteristikum deutlich, das wesensmässig zur Alltagsphysik gehört, nämlich die Schwierigkeit, den von ihr umfassten Stoff auf sinnvolle Weise einzuteilen. Zum einen liegt dies in der schon genannten Interdisziplinarität von Alltagsphänomen begründet, zum andern aber darin, dass uns diese Phänomene in einer Vielzahl von Situationen begegnen, die mit wissenschaftlichen Begriffen und Einteilungen überhaupt inkompatibel sind. Unter welchem Stichwort in einem Physiklexikon sollte man etwa die Tatsache aufführen, dass Gläser häufig trübe werden, wenn sie viele Waschgänge in einer Geschirrspülmaschine hinter sich haben (die Glasoberfläche entwickelt unter der erodierenden Wirkung der Wasserstrahlen mikroskopische Rauhigkeit und verwandelt sich langsam in eine Mattscheibe)? Etwa unter dem Stichwort "Geschirrspülmaschine"?
Haupthilfsmittel zur Erschliessung solcher Begriffe im Lexikon sind das Stichwortregister und Integrationsstichworte. Das Stichwortregister enthält in der Tat auch Begriffe wie "Geschirrspülmaschine" und verweist auf die eigentlichen Lexikonbeiträge, in diesem Falle "Küchenphänomene". Die Integrationsstichworte sind für die Alltagsphysik besonders wichtige Beiträge, deren Sinn sich aus folgender grober Einteilung der Phänomene der Alltagsphysik ergibt:
a) Zum einen kann man physikalische Alltagsphänomene vom Standpunkt wissenschaftlicher Teildisziplinen aus betrachten.
b) Zum anderen lassen sich Ordnungsschemata gemäss Phänomen- oder auch Erlebnisbereichen entwickeln. Für eine Teildisziplin mit Bezug zur Alltagsphysik können als Beispiele Strömungsmechanik oder etwa Physikalische Chemie der Grenzflächen genannt werden; Beispiele für Phänomenbereiche der Alltagsphysik sind Farben und Farberscheinungen oder Geräusche und Töne; Beispiele für Erlebensbereiche der Alltagsphysik sind Haushaltsphänomene und Sport.
c) Schliesslich gibt es noch "Mischformen" physikalischer Alltagsphänomene, die man so auffassen kann, dass sich um bestimmte Phänomen- und Erlebnisbereiche herum (zum Teil recht neue) Teildisziplinen gebildet haben, wie etwa Geo- und Atmosphärenphysik oder Verkehrsphysik.
Vor allem die Klassifizierung nach Phänomen- und Erlebensbereichen erlaubt es, naturwissenschaftliche Alltagserscheinungen gut nach Art und Ort ihres Auftretens zu gruppieren und sinnvoll in einem Stichwort zu integrieren. Abschnitt 2 ist das Kernstück dieses Essays und bietet eine detaillierte Erschliessung der "Alltagsphysik" im Sinne der genannten Einteilung, zusammen mit repräsentativen Beispielen von Alltagsphänomenen; für die meisten der dort besprochenen Stichworte gibt es eigene Lexikonartikel, in denen noch mehr Information zu dem Thema zu finden ist.
Weitere wichtige
Themen der Alltagsphysik sind Formen und Figuren sowie Legenden und Wunder; auf
sie wird im vorliegenden Beitrag nicht näher eingegangen, sie werden als
Integrationsstichworte in eigenen Artikeln behandelt.
2. Erschliessung des Stoffgebietes
2.1 Gruppierung nach Teildisziplinen
Strömungs- und Grenzflächenphänomene
Ein Beispiel für zwei grosse Bereiche der Alltagssphysik sind Strömungs- und Grenzflächenphänomene. Dies zeigen bereits die in der Einleitung erwähnten Beispiele, die entweder etwas mit Strömungen oder mit Grenzflächen zu tun haben. Strömungsphänomene mit grosser Bedeutung für den Alltag sind insbesondere der Bernoulli-, Coanda- und Magnus-Effekt sowie die Turbulenz. Beispielsweise müssen die Kapitäne bei Parallelkurs zwischen zwei Schiffen (etwa beim Betanken oder Umladen) einen Mindestabstand wahren, damit es nicht wegen des Bernoulli-Effektes zu einer Kollision kommt. Ein anderes Beispiel sind die Blutstromgeräusche, die der Arzt bei der Blutdruckmessung mit Manschette abhört und die durch die turbulente Strömung in der verengten Arterie entstehen; die Reynolds-Zahl
(n: kinematische
Viskosität) ist proportional zum Radius r und zur
Strömungsgeschwindigkeit 
, letztere ist proportional zu r - 2 (solange der Blutstrom
einigermassen konstant bleibt), insgesamt steigt also die Reynolds-Zahl mit
fallendem Radius und kann den für Blut kritischen Wert von ca. 103 überschreiten.
In den Bereich der Grenzflächenerscheinungen gehören etwa Kapillarität, Kolloidalität und Osmose, die wiederum eine Vielzahl von Alltagsbezügen aufweisen. So müssen z.B. Frühgeborene u.a. deswegen beatmet werden, weil sie eine lebensnotwendige Substanz noch nicht bilden können, die im Innern (also auf der Luftseite) der Lungenbläschen die grosse Oberflächenspannung der dort immer vorhandenen Wasserschicht auf ein mit der Kraft der Atemmuskulatur verträgliches Mass herabsetzt. Ein anderes Beispiel ist der hohe Binnendruck von "harten" Früchten und Wurzelknollen (z.B. Äpfel, Kartoffeln, Rüben) der durch Osmose entsteht und bis zu 50 bar betragen kann.
Biophysik
Was könnte alltäglicher sein als das Leben? Entsprechend gibt es zwischen Biophysik, Physiologie und medizinischer Physik einerseits und Alltagsphysik andererseits eine besonders starke Verbindung; Beispiele medizinischer Art wurden mit der Oberflächenspannung in den Lungenbläschen und dem turbulenten Umschlag bei den Herztönen bereits genannt. Als Beispiele biologisch-physiologischer Art bzw. Gruppen von solchen sind besonders hervorzuheben:
1. Die
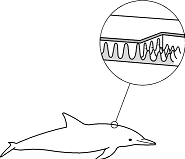
Bewegungsleistungen von Lebewesen: Bei Fischen etwa ist eine erhebliche
Verringerung des Reibungswiderstandes auf die turbulenzdämpfende Wirkung des
viskosen Fischschleimes bzw. der viskoelastischen Fischhaut zurückzuführen ([6]Abb. 1); man erinnere sich daran, dass
Turbulenz einsetzt, wenn Re gross ist, diese ist aber obiger Gleichung
klein, wenn die Viskosität gross ist.
Bemerkenswert ist auch, dass man durch Nachahmen dieser "Tricks" der Natur bei Bootskörpern eine Verringerung des Reibungswiderstand um Faktoren zwei und mehr erzielt hat; solche biologisch-technischen Analogieschlüsse sind Gegenstand der Bionik.
2. Energiebilanz und Stoffwechsel von Lebewesen: Für die Körpertemperatur von Säugetieren etwa ist die Verdunstung von Wasser ein wichtiger Faktor (Verdampfungswärme von Wasser: 2,3 × 106 J/kg, vgl. Grundumsatz des Menschen: 107 J/d); da Hunde keine Schweissdrüsen haben, ist bei ihnen das Schwitzen durch das Hecheln ersetzt.
3. Die Sinnesleistungen von Lebewesen: Zunächst ist hier interessant, dass Spitzenleistungen der Sinnesorgane bei vielen Lebewesen die physikalischen Grenzen weitgehend ausschöpfen. Die Hörschwelle des Menschen [3], [4], [5, S. 1049] von Imin » 4 × 10 - 17 W/cm2 bei der Eigenfrequenz des Gehörgangs n0 » 3 kHz entspricht für eine Periode und dem Trommelfellquerschnitt von A » 0,3 cm2 einer Schwellenleistung und -energie von
Letztere liegt also gerade bei dem thermischen Rauschen mit Eth » 0,025 eV. Für andere Lebewesen (Pmin » 10 - 18 eV z.B. bei der Katze) wird diskutiert, ob diese nicht (unter Einsatz raffinierter Detektionsverfahren) sogar die Grenze zum Quantenrauschen erreichen [6]. Ähnlich können manche Nachttiere Lichtsignale mit einigen wenigen Photonen wahrnehmen, und bei bestimmten Faltern können die Männchen ein einzelnes Molekül des vom Weibchen abgegebenen Sexuallockstoffes riechen. Darüber hinaus stellt man bei immer mehr Lebewesen, z.B. Brieftauben und Zugvögeln, einen magnetischen Sinn fest. Ähnliches gilt für den elektrischen Sinn [7]: Haie z.B. können Felder von wenigen nV/m und damit potentielle Beutetiere durch ihre Aktionspotentiale spüren - eine geradezu an Telepathie grenzende Wahrnehmungsfähigkeit!
4. Kommunikations- und Orientierungsleistungen von Lebewesen: Diese hängen natürlich eng mit den Sinnesleistungen zusammen, bieten aber noch andere physikalische Aspekte. Hier stellen Bienen ein sehr bekanntes Beispiel dar: Ihre Wahrnehmungsfähigkeit für polarisiertes Licht wird erst zusammen mit innerer Verrechnung u.a. der Flugzeit zu einer Möglichkeit, sich auf dem Weg zu Futterplätzen oder Bienenstock orientieren zu können; darüber hinaus haben Bienen bekanntlich auch einen Code (motorischer Art, der sog. "Schwänzeltanz"), um Positionsangaben von Futterplätzen kommunizieren zu können. Solche Kommunikationscodes gibt es auch bei Singvögeln (akustisch) und, zur Partnerfindung, bei Glühwürmchen (optisch, Biolumineszenz); sie können mit Mitteln der Informationstheorie untersucht werden und sind u.a. Gegenstand der Biokybernetik.
Nichtlineare Dynamik
Eine andere, recht junge Disziplin mit sehr intensiven und aktuellen Verbindungen zur Alltagsphysik ist die nichtlineare Dynamik, womit hier der (nicht fest etablierte) Überbegriff für den Gegenstandsbereich zwischen folgenden Forschungsgebieten gemeint ist:
1. Theorie des deterministischen Chaos: Der bekannte Schmetterlingseffekt, dem zufolge der Flügelschlag eines Schmetterlings in Südamerika einen Wetterumschlag in Berlin verursachen kann, beantwortet wenigstens eine der eingangs gestellten Fragen: die nach der Unvorhersehbarkeit des Wetters.
Bleiben wir noch einen
Moment in der freien Natur: [7]Abb. 2 zeigt das steingewordene
Ergebnis der sog. Bäcker-Abbildung, d.h. von wiederholtem Dehnen und Falten wie
bei dem Kneten von Teig. Dies ist eine der Grundformen chaotischer Dynamik, die
anfänglich nahe benachbarte Punkte in unvorhersehbarer Weise auseinandertreibt,
und die Mischung zäher Flüssigkeiten wie Magma ist eine Anwendung.
2. Theorie kritischer Phänomene: Hierzu gehören insbesondere die Phasenübergänge mit ihren alltäglichen Erscheinungsformen wie Schmelzen/Gefrieren und Verdampfen/Kondensieren. Weitere Beispiele sind die Koagulation, etwa das Stocken von Eiweiss bei einer gewissen Grenztemperatur - deswegen darf Fieber auch nicht über 42 °C steigen! - und die kritische Opaleszenz, d.h. der Übergang von durchsichtig nach trübe (etwa in einer Wachsschmelze bei einer bestimmten Temperatur).
3. Synergetik: Viele bekannte Ergebnisse betreffen hier die Musterbildung in unserer alltäglichen Umgebung, beispielsweise die Entstehung von Wolkenstrassen, die sich als walzenförmige Konvektionszellen, wie sie beispielsweise im Bénard-System (Bénardsche Zelle) auftreten, verstehen lassen. Für ein vollständiges Verständnis müssen allerdings noch weitere Faktoren berücksichtigt werden, denn die Zellen im Laborexperiment sind etwa von quadratischem Querschnitt, während sie in der Atmosphäre um einen Faktor bis 50 gestaucht sind [9]. Ein interessanter Ansatz, den u.a. H. Haken [8] in den letzten Jahren verfolgt hat, besteht darin, von Prozessen zur Bildung von Mustern etwas über die Erkennung von Mustern bei der Wahrnehmung zu lernen (und ggf. umgekehrt). In der Tat führt der Ansatz "Mustererkennung ist Musterbildung" zu fruchtbaren Analogien, z.B. zwischen dem aus der Wahrnehmung bekannten Mechanismus der lateralen Inhibition (s.u.) und dem Gierer-Meinhardt-Modell für die Musterbildung bei Muscheln und anderen Lebewesen. Das beiden gemeinsame Prinzip ist der Antagonismus zwischen einer kurzreichweitigen Anregung und einer langreichweitigen Hemmung, wie er z.B. auch zu der Entstehung einer Düne führt: Im Windschatten eines kleinen Hindernisses kommt es zur Ablagerung von Sand (kurzreichweitige Anregung), was in grösserer Entfernung davon zunächst zu einer Verarmung des Sandgehaltes in der Luftströmung führt (langreichweitige Hemmung); erst wenn vom Boden wieder ausreichend Sand mitgerissen wurde, kann es zur Bildung einer neuen Düne kommen.
Mathematik
Schon durch die vorangehenden Beispiele erscheint es vielleicht nicht mehr so überraschend, dass es auch interessante Verbindungen zwischen Alltagsphysik und Mathematik gibt. Höchst alltäglich ist z.B. die Normalverteilung. Man findet sie durch einfaches Zählen für die Grössenverteilungen von Lebewesen, Werkstücken und Messergebnissen, und bei der immensen Bedeutung dieser Verteilung sollte der Grund für deren Allgegenwart - der zentrale Grenzwertsatz der Statistik - jedem Physiker geläufig sein. Zahlentheorie, Katastrophentheorie und Knotentheorie sind weitere Beispiele mathematischer Teildisziplinen mit alltagsphysikalischen Anwendungen.
Daneben gibt es noch
eine ganz andere Weise, wie auf der Ebene von Alltagsbeobachtungen erhellende
Verbindungen zwischen Mathematik und Physik hergestellt werden können, nämlich
zur Veranschaulichung von abstrakten Sachverhalten per Analogie zu einfachen
Phänomenen. [8]Abb. 3 zeigt, wie Sie z.B. die
Nichtkommutativität von Operatoren konkret nachvollziehen können, und ein
weiteres Beispiel betrifft die geometrischen Phasen: Lassen Sie Ihren Arm frei
hängen und richten Sie den Daumen nach vorne. Führen sie dann mit dem Arm
folgende Abfolge von Bewegungen durch, ohne die Hand dabei zu verdrehen: erst
seitlich bis auf Schulterhöhe heben; dann auf der gleichen Höhe bis vor die
Augen bewegen; schliesslich zurück in die Ausgangsposition senken. Schauen Sie
nun auf Ihren Daumen: er deutet jetzt zum Bein, während er doch anfangs nach
vorne wies. Der Daumen und mit ihm die Hand haben sich also um 90° gedreht, obwohl Sie zu jedem
Zeitpunkt darauf geachtet hatten, dass sie sich nicht drehen. Die festgestellte
Drehung ist gerade so gross wie der von dem Weg ihrer Hand umschlossene
Raumwinkel; der Effekt beruht auf der Abweichung der Winkelsumme von Dreiecken
auf der Kugel von 180°,
und das gefundene Ergebnis lässt sich auf allgemeine Wege auf der Kugel
verallgemeinern. Die geometrischen Phasen der Quantenphysik sind genau in
demselben Sinne und aus demselben Grunde "geometrisch" wie der eben
besprochene Winkel auf der Kugeloberfläche; für Zwei-Zustands-Systeme lässt sich
dies direkt und im allgemeinen Fall per Analogieschluss zeigen.
2.2 Gruppierung nach Phänomenbereichen
Optische Erscheinungen
Buchstäblich allgegenwärtig sind die durch unsere Sinne wahrgenommenen Phänomene, und Farben und Farberscheinungen spielen hier, im Hinblick auf die Tatsache, dass ein grosser Teil aller Informationen auf optischem Weg ins Gehirn gelangen, eine besondere Rolle. Wer hätte z.B. noch nicht beobachtet, dass viele poröse Materialien wie Erde, Holz, Textilien dunkler erscheinen, wenn sie feucht sind? Wenn die Zwischenräume der Poren mit Wasser gefüllt sind, wird das Licht weniger gestreut, denn die Brechzahl von Wasser ist höher als diejenige von Luft und liegt daher näher bei der Brechzahl der festen Grenzflächen; kleinere Unterschiede in der Brechzahl aber bedeuten weniger Streuung, das Licht dringt also tiefer in das Material ein. Grössere Eindringtiefe bedingt nun wiederum gemäss dem Lambert-Beerschen Gesetz exponentiell grössere Absorptionsverluste, d.h. das Material erscheint dunkler. Ein anderes sehr schönes Beispiel für eine optische Phänomengruppe liefern die Interferenzfarben, die eine gemeinsame Grundlage für die schillernde Vielfalt der Farberscheinungen von Ölfilmen, Seifenblasen, Insektenpanzern, Schmetterlingsflügeln, Vogelfedern, Perlmutt und Opalen bilden.
Eine weitere Gruppe von besonders faszinierenden optischen Alltagsphänomenen sind optische Täuschungen.
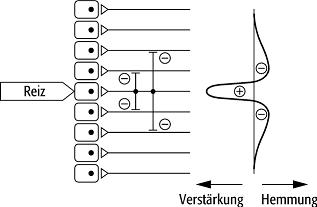
[9]Abb. 4 a zeigt die
Machschen Flecken, dunkle Stellen in den Kreuzungen der hellen Steifen, die man
wie folgt erklärt: Fällt Licht auf einen Punkt der Netzhaut, so umgibt den
kurzreichweitigen Bereich der Anregung ein langreichweitiger Bereich der
Hemmung ([10]Abb.
4 b); in den Kreuzungen von zwei weissen Streifen gibt es doppelt so
viele hemmende Nachbarzellen wie in einem einzelnen Streifen, und deswegen
erscheinen diese Stellen dunkler. Dieser Mechanismus, das Prinzip der lateralen
Inhibition, hat als fundamentale Grundform von Prozessen in der Synergetik
(s.o.) sehr grosse Bedeutung gewonnen [4].
Akustische Erscheinungen
Eine akustische
Phänomengruppe, die im Alltag häufig mehr als lieb präsent ist, ist die der
Geräusche und Töne. Ein eher angenehmer Fall ist hier das "Singen"
von Gläsern ([11]Abb. 5). Der Anregungsmechanismus ist
der von Reibungstönen, d.h. durch den Unterschied von Haft- und Gleitreibung
verursachte Kippschwingungen.
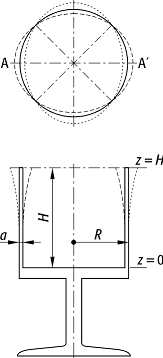
Die Grundfrequenz ist für ein zylindrisches leeres Glas gegeben durch
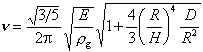
wobei der erste
Wurzelfaktor die Abhängigkeit von den Materialeigenschaften (Elastizitätsmodul E
und Dichte rg) enthält, und die
anderen Funktionen die Abhängigkeit von geometrischen Eigenschaften (Radius R,
Höhe H und Wanddicke D des Glases); dabei rührt der Faktor D/R2 von der horizontalen
Verbiegung her, und die zweite Wurzel stellt einen Korrekturfaktor für die
zusätzliche vertikale Verbiegung dar. Für ein mit der Flüssigkeit der Dichte rf bis zur Höhe H ¢ gefülltes Glas ist n durch eine
näherungsweise zu 
proportionale "Füllkorrektur" zu
dividieren, die im wesentlichen als "Trägheitskorrektur" durch die
zusätzliche Masse der Flüssigkeit zu verstehen ist; sie besagt, dass ein Glas um
so tiefer klingt, je höher es gefüllt ist.
Ein weniger angenehmer
Fall ist das "Singen" von Reifen, wie es an gelegentlich im
Strassenbelag eingefrästen periodischen Querrillen auftritt, wobei die Frequenz
durch v = 
/d gegeben ist (
:
Fahrzeuggeschwindigkeit, d: Rillenabstand); damit nicht der Reifen schon
ohne Querrillen "singt", sind die Profilstollen nicht periodisch
angeordnet.
Interessanterweise gibt es auch akustische Täuschungen. Sie sind zum Teil sehr störender, ja qualvoller Art, wie das bekannte "Klingeln" in den Ohren. Dies ist nicht immer nur ein Scheinsignal (z.B. auf eine Überlastung des Ohres zurückzuführen), sondern es handelt sich oft um ein reales Signal mit einem ausserhalb des Ohres messbaren Schalldruckpegel. Solche Eigengeräusche des Ohres sind eine Folge der beim Hörvorgang ablaufenden aktiven Verstärkung des Schallsignals [4].
Wasserwellen
Ein anderer Bereich,
wo Wellenphänomene im Alltag stark in Erscheinung treten, sind Wasserwellen.
Beispielsweise lässt sich hinter einem überströmten Stauwehr oder hinter einem
Felsen in einem Bach oft eine - häufig sehr ausgeprägte und stark schäumende -
stehende Welle beobachten. Diese wird als Wassersprung bezeichnet, und sie ist
darauf zurückzuführen, dass in einer Querschnittsverengung die Strömungsgeschwindigkeit
so stark zunehmen kann, dass sie die
Wellenausbreitungsgeschwindigkeit c im Wasser übersteigt; stromabwärts
von der Verengung muss es also eine Stelle geben, wo die beiden
Geschwindigkeiten gerade übereinstimmen. Da sich an dieser Stelle Störungen mit
Strömungsgeschwindigkeit gegen die Strömung und also mit Geschwindigkeit Null
gegen das Ufer bewegen, addieren sich deren Wirkungen zu der schäumenden,
stehenden Welle des Wassersprungs. Entscheidend ist, wie bei vielen
Strömungsphänomenen, auch hier eine dimensionslose Kennzahl, und zwar die
Froude-Zahl Fr = 
/c. Ein
weiteres physikalisch interessantes Beispiel sind die Tsunamis, durch Seebeben
oder Vulkanausbrüche ausgelöste turmhohe Seewellen, deren Reichweite von vielen
hundert Kilometern durch ihren Charakter als Solitonen erklärlich wird, d.h.
durch die Kompensation des Zerfliessens des Wellenpaketes durch
Nichtlinearitäten des Ausbreitungsprozesses.
Bruchmechanik
In der Bruchmechanik
beschäftigt man sich mit einer Form von Zerstörung, die leider nur zu
alltäglich ist, aber physikalisch interessante Hintergründe hat, nämlich mit
der Bildung von Rissen und Brüchen in festen Materialien. Ein Beispiel für eine
sehr elementare Betrachtung eines bruchmechanischen Phänomens ist, dass aus
einer einfachen Energiebetrachtung die Existenz einer kritischen Länge folgt,
der Griffith-Länge lG
~
sB/eS (sB, Brucharbeit pro Fläche
in J/m2, eS mittlere
Spannungsenergie pro Volumen in J/m3), ab der für das Wachstum von Rissen
Selbstverstärkung einsetzt; ein anderes Beispiel ist die fraktale Struktur von
Bruchkonturen.
2.3 Gruppierung nach Erlebensbereichen
Haushaltsphänome
Zwei Bereiche
alltäglichen Erlebens, in denen der aufmerksame Blick viel Physik entdecken
kann, sind die der Haushaltsphänomene (einschliesslich Haushaltstechnik), etwa
Lichtquellen und der Küchenphänomene (einschliesslich Nahrungsmittel). Warum
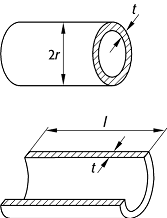
beispielsweise platzen Würstchen beim Erhitzen immer in Längsrichtung? Weil die
Wandspannung in einem unter den Druck p gesetzten Rohr (Radius r,
Länge l, Wanddicke t) in axialer Richtung rp/2t, in
tangentialer Richtung aber doppelt so gross ist; dies folgt, wenn man die durch
den Druck auf einen radiale bzw. axiale Querschnittsfläche erzeugte Kraft (pr2p bzw. 2rlp)
durch die Wandflächen in diesen Querschnittsebenen (2prt bzw. 2lt)
teilt ([12]Abb. 6).
Dass wir ganz allgemein
Küche und Nahrung als einen Teilbereich besonders intensiven Erlebens
empfinden, hat neben dem offensichtlichen biologischen auch einen
physikalischen Grund: Der Küchenherd sorgt gewissermassen für eine exponentielle
Intensivierung, da viele Reaktionsraten dem Arrhenius-Gesetz gehorchen und
proportional zu einem Faktor 
(T: Temperatur, Ea: Aktivierungsenergie, kB: Boltzmann-Konstante)
sind, so dass die Anzahl und Ausbeute der relevanten Prozesse sehr stark mit der
Temperatur steigt.
Spiel und Sport
Zwei weitere
Erlebensbereiche mit viel Bezug zur Physik sind Spielzeug und Sport. Das
Mariottesche Stosspendel (vulgo "Klick-Klack-Maschine") beispielsweise
dient regelmässig zur Illustration der Energie- und Impulserhaltung; weniger
bekannt ist, dass sich durch die unvermeidlichen Dissipationsverluste mit der
Zeit eine Situation einstellt, in der alle Kugeln synchron schwingen und keine
Stösse mehr stattfinden. Der Grund hierfür lässt sich wie folgt einsehen: Die zeitliche
Entwicklung eines Systems unter Stössen lässt sich durch eine lineare Abbildung
beschreiben, für die es, analog zu Schwingungen, Normalmoden gibt; sind die
Stösse dissipativ, so hält die Mode mit der kleinsten Dämpfung am längsten an,
und dies ist für identische Teilchen gerade die synchrone Bewegung, weil es
dabei keine Stösse und damit keine Dissipation durch solche gibt (die Reibung an
der Luft sowie in der Aufhängung bleibt natürlich). Ein anderes Beispiel im
Zwischenbereich zwischen Spiel und Sport ist der Magnus-Effekt, der sowohl für
die Frisbee-Scheibe wie für die "geschnittenen" Bälle beim Fussball,
Golf und Tennis/Tischtennis sehr wichtig ist. Dasselbe gilt für den
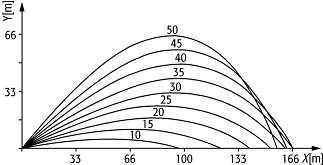
Luftwiderstand; [13]Abb. 7 zeigt beispielsweise die
Flugbahn eines Golfballes unter dem Einfluss der Schwerkraft mg und
Stokes\'scher Reibung k
, wofür die
Lösung der Newtonschen Gleichungen
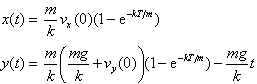
lautet (m:
Masse, 
:
Geschwindigkeit des Balles, k: Reibungskonstante, g:
Erdbeschleunigung). Das Ergebnis erinnert sehr an die mittelalterliche Darstellung
von ballistischen Kurven ([14]Abb. 8).
2.4 Mischformen
Mehrere Phänomen- bzw.
Erlebensbereiche umfassen so viele und so wichtige Verbindungen zur Physik, dass
sie zugleich Gegenstand eigenständiger wissenschaftlicher Teildisziplinen sind.
Ein klassisches Gebiet dieser Art ist die Geo- und Atmosphärenphysik. Als
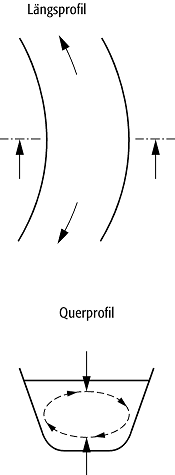
geophysikalisches Alltagsfaktum ist beispielsweise das Baer-Babinetsche Gesetz
zu nennen, wonach bei den Flüssen der Nordhalbkugel - bei sonst symmetrischen
geographischen Bedingungen - das rechte Ufer stärker unterspült, daher also
steiler ist als das linke (auf der Südhalbkugel sind die Rollen vertauscht):
Durch die Coriolis-Kraft bekommt die Strömung eine zur Strömungsgeschwindigkeit
proportionale, nach rechts gerichtete
Beschleunigungskomponente, und da 
wegen der Bodenreibung mit zunehmender
Wassertiefe abnimmt, setzt eine quer zur Strömung gerichtete
Zirkulationsströmung ein, bei der das linke Ufer ("Gleithang") mit
langsamen Wasser aus Bodennähe und das rechte ("Prallhang") mit
schnellerem Wasser aus höheren Schichten angespült und also stärker erodiert
wird [15]Abb. 9).
Als stark
anwendungsorientierte Gebiete sind hier die Bauphysik, die Verkehrsphysik sowie
Materialwissenschaft und Verfahrenstechnik zu nennen. Ein Beispiel
verkehrsphysikalischer Art wurde mit den "singenden" Reifen oben
schon genannt. Materialwissenschaftlich hochinteressante Alltagsmaterialien
stellen z.B. Holz und Knochen dar. Sie sind Beispiele "intelligenter"
Werkstoffe, die ihr Gefüge in Abhängigkeit von der Belastung auf grössere
Stabilität hin selbsttätig anpassen können. Die heutige Technik kann hier das
Vorbild Natur nur sehr unvollkommen nachahmen; will man z.B. bei Druck- oder
Biegebelastung einer Säule einen der Faktoren Höhe, Gewicht oder Tragkraft der
Säule optimieren, so muss man einen möglichst grossen Wert der Kenngrösse E/r2 (E:
Elastizitäsmodul, r: Dichte) haben, bei der Holz nur noch von
Diamant übertroffen wird.
3. Weiterführende Überlegungen, Ausblick auf offene Fragen
Anhand der vorangehenden Beispiele wird deutlich, dass sich physikalische Alltagsphänomene in zwei Stufen präsentieren, sozusagen auf den ersten oder auf den zweiten Blick. Dass das Singen von Weingläsern etwas mit Physik, genauer Akustik zu tun hat, ist offensichtlich - ein Fall von Alltagsphysik auf den ersten Blick. Zunächst sehr fernliegend erscheint aber der Gedanke, dass das Dunkel der Nacht ein physikalisches erklärungsbedürftiges Phänomen darstellt (Olbers\'sches Paradoxon).
Dass sich dahinter - ca. 15 Mrd. Lichtjahre "dahinter" - die endliche Ausdehnung und das endliche Alter des Kosmos verbergen, empfinden wir als höchst faszinierend und staunenswert - ein Fall von Alltagsphysik auf den zweiten Blick.
Es ist eine eigene
Fähigkeit, das Besondere und Hinterfragenswerte im Alltäglichen sehen und vom
scheinbar Banalen auf das Fundamentale schliessen zu können. V. Weisskopf hat
durch eine ihm eigene Art von Grössenordnungsargumenten gezeigt [10], wie die
Grösse von Wassertropfen und Bergen auf den Wert des Planckschen
Wirkungsquantums zurückgeführt werden kann: die Schwereenergie pro Molekül ES = Ampgh (A
Massenzahl, mp
Protonenmasse) muss kleiner sein als die Energie pro Molekül, die nötig ist, um
in einem Stoff plastisches Fliessen zu hervorzurufen. Diese Energie ist ein
Bruchteil a
der Schmelzwärme, die Schmelzwärme wiederum ein Bruchteil b der mittleren
Bindungsenergie pro Elektron und diese schliesslich ist ein Bruchteil g
der Bohrschen Energie EB » 13,6 eV, so dass sich also insgesamt ergibt: ES
abgEB oder
Hier ist der zweite
Bruch ein Quotient aus einer Energie und einer Kraft, hat also in der Tat die
Dimension einer Länge, und das Wirkungsquantum steckt in 
. Für Quarz (SiO2) lauten die
Tabellenwerte für Schmelz- und Bindungsenergie 0,15 eV bzw. 6,5 eV, d.h. b
= 0,023 und g = 0,48; nimmt man a = 1, so ergibt sich
als Maximalhöhe ca. 20 km, was von der Grössenordnung her gut mit der Höhe des
Mt. Everest übereinstimmt. Übrigens lassen sich die Werte von b
und g
selbst wieder aus einfachen Abschätzungen gewinnen, und der Wert von a
birgt schon eine erste Korrektur der Höhe nach unten, denn für plastisches
Fliessen muss die Kristallstruktur weniger aufgelöst werden als für vollständiges
Schmelzen, also a < 1. Die Maximalgrösse von Wassertropfen ergibt sich aus einem
ähnlichen Vergleich der Oberflächenenergie mit der Schwereenergie zu ca. 0,5
cm. Faszinierend ist, dass darüber hinaus auch die schiere Existenz und
Stabilität der Materie im Grossen ein buchstäblich mit den Händen zu greifendes,
makroskopisches Quantenphänomen darstellt, denn ohne Pauliprinzip würde sie mit
zunehmender Teilchenzahl unter Aussendung gewaltiger Energiemengen implodieren
[11]. Dies ist ein Beispiel für die zunächst sehr unvermutete Verbindung
zwischen Alltagsphänomenen und Quantenphysik. Ein weiteres Beispiel hierfür ist
das Leuchten der Sonne, denn ohne Tunneleffekt gäbe es in Sternen keine
Kernfusion. Eng verwandt mit den Weisskopf-Argumenten sind die Fermi-Fragen,
beispielsweise: Ist es möglich, dass das Blut eines Erwachsenen noch Atome
seiner Mutter enthält? Wenn ja, wieviele? Betrachten wir z.B. Natrium, wovon
ein Mensch - ganz grob - 100 g insgesamt enthält und 3 g täglich benötigt (laut
Ernährungstabellen). Es werden demnach pro Tag ca. 3% verstoffwechselt,
entsprechend einer Halbwertszeit von ca. 23 Tagen. Also gibt es von den
anfänglich rund 2,6 × 1024 Natrium- Atomen nach fünf Jahren kein
einziges mehr. Ein Erwachsener hat nach wenigen Jahren alle Natriumatome in
seinem Blut (und dem damit im Gleichgewicht stehenden Gewebe) restlos durch
Stoffwechsel ausgetauscht. Anders verhält es sich mit dem wesentlich fester
gebundenen Natrium und auch Kalzium im Skelett; für letzteres hat G.v. Hevesy
mit radioaktiven Markierungmethoden (für die er den Nobelpreis erhalten hat)
bei Mäusen nachgewiesen, dass es über mehrere Generationen weitervererbt wird.
Ähnliches gilt auch für den Menschen, d.h. ein Mensch enthält Kalziumatome
nicht nur der Mutter, sondern mindestens der Urgrossmutter.
Weisskopf-Argumente,
Fermi-Fragen, oder, um mit de Gennes zu sprechen, der Franklinsche Geist,
stehen zunächst für die immense fachdidaktische Bedeutung von
Alltagsphänomenen, die z.B. in den Beispielsammlungen [12], Lehrerzeitschriften
[13] und dem Lehrbuch [5] in hervorragender Weise zum Tragen kommt. Neben der
enormen Motivationswirkung durch den starken Bezug zu Alltag und Anwendung
zeichnet sich diese Art von Physik durch einen ausgeprägten Gebrauch von
Analogie-, Dimensions- und Grössenordnungsdenken aus: Analogien, die zwischen
dem Alltäglichen, Anschaulichen und dem Abstrakten eine Brücke bilden wie in [16]Abb. 4, oder die erkenntnisleitende
Denkform ganzer Teildisziplinen wie der Bionik sind; Dimensionsbetrachtungen,
die z.B. in dem völlig unübersichtlichen Fahrwasser der Strömungsmechanik ein
geistiger Rettungsanker sind; und Grössenordnungsdenken als A und O jeden
Experimentes und jeder Theorie. Dies bedeutet dann aber auch, dass die Physik
gerade in ihren alltäglichen Anwendungen eine allgemeine Schule des Denkens
bietet, nämlich für einen durch aufmerksame Beobachtung und - einfache! -
Mathematik erheblich geschärften gesunden Menschenverstand.
Schliesslich bietet die
Alltagsphysik nicht nur für die Lehre, sondern auch für die Forschung ein heute
noch längst nicht erschöpftes Potential, und hier schliesst sich der Kreis zu
den Eingangsfragen: Es ist bemerkenswert, dass gerade eine der Erscheinungen,
die am Anfang der wissenschaftlichen Beschäftigung mit elektrischen
Erscheinungen stand, nämlich die Reibungselektrizität, auch heute noch sehr
unvollkommen verstanden ist. Es ist ausserdem bemerkenswert, dass bei einer
ebenfalls allgegenwärtigen Erscheinung, der Turbulenz, erst seit jüngster Zeit
von einem auch nur annähernden Verständnis die Rede sein darf [14]. Und es ist
überraschend und erfrischend, dass ein afrikanischer Schuljunge beim Eismachen
eine Beobachtung machen konnte, die zwar auch Aristoteles schon bekannt war,
die die Wissenschaft aber bis in heutige Zeit nicht geklärt, wenn nicht
überhaupt abgestritten hat: der Mpemba-Effekt, d.h. die Tatsache, dass heisses
Wasser unter Umständen schneller gefriert als kaltes. Dabei spielen mindestens
ein halbes Dutzend durchaus nichttrivialer Faktoren eine Rolle, von der
Löslichkeit von Luft bist zu der Unterkühlung des Wassers [15]. Der Effekt
erschöpft sich also keineswegs in der Trivialität, dass von heissem Wasser mehr
verdunstet und also weniger gefrieren muss, und Mpemba hat diesen und einen
weiteren naheliegenden Grund durch Experimente ausgeschlossen, die er trotz des
Spottes seines Physiklehrers und seiner Mitschüler durchführte. Er zeigte dabei
jene wertvolle Fähigkeit, im Dunkel der Nacht ebenso wie im Leuchten der Sterne
etwas Hinterfragenswertes zu erkennen und die eigenen Fragen auch ernst zu
nehmen, die Fähigkeit, die P.-G. de Gennes den Weg von der Alltagsphysik bis
zum Nobelpreis führte und die er so umschreibt: "Staunen können über einen
Wassertropfen".
Literatur
[1] P.G. de Gennes, J.
Badoz: Les Objets Fragiles, Librairie Plon, Paris 1994.
[2] P.G. de Gennes, Rev. Mod. Phys. 57 (1985) 827.
[3] H.-P. Zenner, A. Gitter, Physik in unserer Zeit 18 (1987) 97.
[4] M. Euler, Biologie in unserer Zeit 26 (1996) 163 u. 304.
[5] H. Vogel: Gerthsen Physik, Springer, Heidelberg 1995.
[6] W. Bialek, A. Schweitzer, Phys. Rev. Lett. 54 (1985) 725
[7] J. Bastian, Phys. Today (Feb. 1994) 30.
[8] H. Haken, M. Stadler (Hrsg.): Synergetics of Cognition, Springer,
Berlin-Heidelberg-New York 1989.
[9] M.G. Velarde, C. Normand, Spektrum der Wissenschaft (Sept. 1980)
118.
[10] V. Weisskopf, Science 187 (1975) 605; Am. J. Phys. 53
(1985) 19 und 54 (1986) 110.
[11] W. Thirring, Die Naturwissenschaften Bd. 73 (1986) 605-613.
[12] J. Walker: The Flying Circus of Physics, John Wiley & Sons, New
York 1977, und die Beiträge Experiment des Monats in Spektrum der
Wissenschaft; C.P. Jargocki: Eigentlich klar - Oder? Selbstverständliches
physikalisch erklärt, Vieweg, Braunschweig 1986; I.K. Kikoin (Hrsg.): Physik:
Experimentieren als Spielerei, Spektrum, Heidelberg 1991.
[13] W. Kuhn (Hrsg.): Praxis der Naturwissenschaften: Physik,
Aulis-Verlag/Deubner und Co., Köln.
[14] S. Grossmann, Phys. Bl. 51 (1995) 641.
[15] D. Auerbach, Am. J. Phys. 63 (1995) 882 und Spektrum der
Wissenschaft (Apr. 1996) 15.
Alltagsphysik 1:
Turbulenzdämpfung in der Delphinhaut.
Alltagsphysik 2:
Das steingewordene Ergebnis der Bäcker-Abbildung.
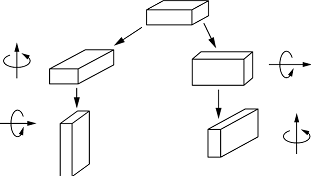
Alltagsphysik 3:
Nichtkommutativität: Unterschiedliche Reihenfolge von Drehungen bewirkt
unterschiedliches Endergebnis.
Alltagsphysik 4: Machsche Flecken (oben) und Prinzip der lateralen Inhibition (unten).
Alltagsphysik 5:
Elliptische Verformung als Grundmode des "singenden Weinglases". Oben
die resultierende Verbiegung in horizontaler, unten in vertikaler Richtung.
Alltagsphysik 6:
Zum Platzen eines Würstchens.
Alltagsphysik 7:
Einfluss von Reibung auf ballistische Kurven; Parameterwahl c/m = 0,25 s - 1 entspricht empirischen Werten für
Golfball.
Alltagsphysik 8:
Mittelalterliche Darstellung ballistischer Kurven; so falsch nicht!
bottom:.0001pt;border:none; mso-border-left-alt:solid purple 1.5pt;mso-border-bottom-alt:solid purple 1.5pt; mso-border-right-alt:solid purple 1.5pt;padding:0cm;mso-padding-alt:0cm 13.0pt 13.0pt 13.0pt\'>Alltagsphysik 9: Das Baer-Babinetsche Prinzip: In Bodennähe ist die Coriolis-Beschleunigung kleiner als in den höheren Wasserschichten, so dass eine Zirkulationsströmung einsetzt.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.