Techniklexikon

Auflösungsvermögen

Als Auflösungsvermögen bezeichnet man die Fähigkeit einer optischen oder elektronisch-optischen Abbildungs- oder Wiedergabevorrichtung, zwei räumlich getrennte Punkte oder parallele Linien gerade noch als getrennt erkennbar abzubilden oder wiederzugeben. Da das Auflösungsvermögen moderner Spitzenobjektive das fotografischer Emulsionen übertrifft, wirken sich als begrenzende Faktoren für die optimale Auflösung lediglich die Eigenschaften des Filmmaterials aus. Ein Maß für das Auflösungsvermögen fotografischer Schichten finden wir in der Anzahl der abgebildeten Linien pro Millimeter, die gerade noch getrennt wiedergegeben werden können: je mehr Linien, desto größer das Auflösungsvermögen. Da das Auflösungsvermögen seine Grenzen in der Korngröße einer Filmemulsion hat, ist seine Abhängigkeit von der Empfindlichkeit eines Films nur logisch. Zum Beispiel haben hochempfindliche Schwarzweißfilme ein Auflösungsvermögen von ca. 80 Linien/ mm, mittelempfindliche ca. 120 Linien/ mm und niedrig empfindliche Filme (15 DIN) sogar bis zu 200 Linien/mm. Gute Farbumkehrfilme liegen, bedingt durch ihre zahlreichen Schichten (die zu einer höheren Gesamtschichtdicke führen) mit einem Auflösungsvermögen von ca. 125 Linien/mm (bei 19 DIN) etwas unter dem Leistungsvermögen von Schwarzweißfilmen. Da sich Uber-belichtung und Überentwicklung nachteilig auf die Größe des Korns auswirken, ist im Interesse eines maximalen Auflösungsvermögens auf exakte Belichtung und Entwicklung (Feinkornentwickler) zu achten. Mass für den geringsten Abstand zweier Beobachtungswerte bzw. Beobachtungsobjekte, die von einer Beobachtungs- bzw. Messeinrichtung mit Sicherheit getrennt registriert werden können.

1) Optisches Auflösungsvermögen

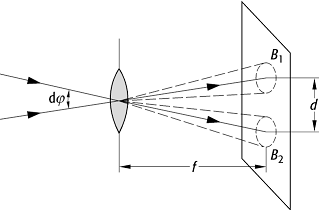
Beim Eintritt der von einem Objekt ausgehenden Lichtstrahlen in ein optisches System kommt es zu Beugungserscheinungen (Beugung) an der Begrenzung des optischen Gerätes, z.B. am Rand der Eintrittspupille. Ein entfernter Lichtpunkt wird daher nicht als Punkt (Beugung), sondern als Beugungsscheibchen (Airy-Scheibchen) mit dem Radius r = 1,22 lf/D abgebildet, umgeben von mehreren nach aussen sehr schnell an Intensität verlierenden konzentrischen schmalen Kreisen (l ist die verwendete Wellenlänge, f die Brennweite und D der Durchmesser der Linse). Es fallen etwa 84 % des gesamten Lichts auf die Airy-Scheibe, innerhalb des zweiten dunklen Rings liegen 91 % des Lichts. Sollen zwei Objekte abgebildet werden (Abb.), die vom Objektiv aus gesehen einen Winkelabstand von dj haben, so gelten diese als auflösbar, wenn bei den Beugungsscheibchen das Helligkeitsmaximum des einen Objekts auf dem ersten Helligkeitsminimum des anderen zu liegen kommt, d.h. wenn die beiden Helligkeitsmaxima keinen geringeren Abstand als d = 1,22 lf/D haben (Rayleigh-Kriterium). Da dieser Abstand gleich f dj ist, folgt dj = 1,22 l/D. Diese Grösse wird Auflösungsgrenze genannt; sie ist der Kehrwert des Auflösungsvermögens U, für das somit gilt U = 1/dj = 0,82 D/l. (Beide Begriffe werden oft fälschlicherweise synonym verwendet.) Das Auflösungsvermögen ist also um so grösser, je kleiner die Wellenlänge und je grösser der Objektivdurchmesser ist. Diese Überlegungen gelten sowohl für das Teleskop wie auch für das menschliche Auge (siehe unten). Bei Mikroskopen unterscheidet man das laterale Auflösungsvermögen, also das Auflösungsvermögen für seitlich ausgedehnte Strukturen, und das Tiefenauflösungsvermögen, das sich auf die Tiefenstruktur bezieht. Zur Bestimmung des lateralen Auflösungsvermögens wird der Mindestabstand der Beugungsscheibchenmittelpunkte mit d = 1,22l/A beziffert, wobei A die numerische Apertur des Objektivs ist (A = R/f mit R: Radius des Objektivs, f: Brennweite des Objektivs). Da in der Mikroskopie Unterschiede in Form und Helligkeit die Fähigkeit des Auges zur Auflösung von Strukturen wesentlich beeinflussen, führt man noch einen physiologischen Faktor k ein. Das praktische Ergebnis ist, dass zwei Teilchen noch voneinander getrennt beobachtet werden können, wenn ihr Abstand ungefähr l/2 beträgt, vorausgesetzt, die numerische Apertur hat etwa den Wert 1. Das Auflösungsvermögen ist auch hier gleich dem Reziproken der Auflösungsgrenze d, also ist U = 1/d = 0,82 × k × A/l. Beim Interferenzmikroskop ist das Auflösungsvermögen ein Phasenauflösungsvermögen, da die Tiefenstruktur als Phasenverschiebung beobachtet wird. Das Phasenauflösungsvermögen beträgt für Auflicht etwa 20/l, für Durchlicht 10/[(n - 1)l] (dabei ist n die Brechzahl des Objekts). Die Phasenauflösung kann nur auf Kosten der Seitenauflösung verbessert werden. Da das Auflösungsvermögen umgekehrt proportional zur Wellenlänge ist, kann es durch die Verwendung von kurzwelligerem Licht verbessert werden (Ultraviolettmikroskopie, Elektronenmikroskopie). Bei der Immersionsmikroskopie kann die Einbettung des Objekts in ein optisches Medium mit grosser Brechzahl die numerische Apertur und damit das Auflösungsvermögen erhöhen.

Ein weiterer wichtiger Parameter ist die Beleuchtung. Während man bei Teleskopen und beim Auge vom Auflösungsvermögen für selbstleuchtende Objekte (Helmholtzsches Auflösungsvermögen) spricht, hat Abbe das Auflösungsvermögen für nichtselbstleuchtende Körper untersucht (hauptsächlich in Bezug auf die Mikroskopie). Nach Abbe beruht die Bildentstehung auf der Beugung des Lichts, wobei vor allem die erste Beugungsordnung für die Bildentstehung wesentlich ist. Die Abbildungsqualität ist dann beugungsbegrenzt, wenn die erste Beugungsordnung das Gerät nicht mehr ungestört durchläuft. Über die Beziehung sinj = l/d für den Winkel der ersten Beugungsordnung erhält man den minimalen Abstand zweier aufzulösender Objektpunkte zu d = l/(n sin a) = l/A mit a als Objektivöffnungswinkel und A als numerische Apertur. Das daraus resultierende Auflösungsvermögen U = 1/d = A/l ist damit um den Faktor 1,22 grösser als das Auflösungsvermögen für selbstleuchtende Objekte (s.o.), wenn man zusätzliche physiologische Korrekturfaktoren vernachlässigt. Vom Standpunkt der modernen Optik her besteht aber kein prinzipieller Unterschied zwischen der Helmholtzschen und der Abbeschen Vorstellung des Auflösungsvermögens.

2) Spektrales Auflösungsvermögen

Bei Spektralapparaten wird die Grösse U =  l/Dl als Auflösungsvermögen definiert. Sie gibt die Fähigkeit des Spektralapparates an, für Lichtwellen nahe beieinanderliegender Wellenlängen die Intensitätsmaxima nach Durchgang durch den Apparat räumlich zu trennen. Die wellenlängenselektiven Parameter (z.B. Brechzahl eines Prismas, Beugungswinkel eines Gitters, ...) sind bei diesen optischen Geräten i.a. nicht linear von der Wellenlänge abhängig. Strenggenommen muss darum das Auflösungsvermögen explizit für eine Wellenlänge oder ein schmales Wellenlängenintervall angegeben werden. Bei Beugungsgittern gelten zwei Wellenlängen l₁ und l₂ = l₁ + Dl dann als getrennt, wenn das Interferenzmaximum von l₁ in ein Minimum von l₂ fällt (bzw. der Abstand der Interferenzmaxima grösser ist als ihre Halbwertsbreite). Die Halbwertsbreite der Interferenzmaxima eines Gitters nimmt mit höherer Ordnung ab, das Auflösungsvermögen also zu. Es gilt l/Dl = pk, wobei k die Beugungsordnung und p die Zahl der beleuchteten Striche ist. Während die beobachtbare Gitterordnung durch die mit höherer Ordnung abnehmende Intensität der Maxima beschränkt ist, kann man das Auflösungsvermögen eines Gitters auch durch die Zahl der kohärent beleuchteten Gitterspalte beeinflussen. Ein typisches Transmissionsgitter hat ca. 600 Striche pro Millimeter. Bei einer beleuchteten Breite von 16 cm ergibt dies für p » 100 000. Beobachtet man in der dritten Beugungsordnung, erreicht man ein Auflösungsvermögen von ca. 300 000. Zum Vergleich: der Wellenlängenabstand der beiden Na-D-Linien beträgt l/Dl » 1000. Für noch höhere Auflösungen kann man die beleuchtete Breite noch weiter erhöhen oder den Abstand der Striche verringern. Die besten Rowland-Gitter haben bis zu 1700 Striche pro Millimeter, holographische Gitter z.T. sogar mehrere tausend. Aufgrund der hohen Anforderungen an die Oberflächengüte wächst hier aber der Herstellungsaufwand für Auflösungen grösser als 300 000 enorm.

Das spektrale Auflösungsvermögen eines Prismas ist gegeben durch l/Dl = bdn/dl, wobei b die Basislänge und dn/dl die Dispersion des Prismas ist. Nach den Prinzipien der geometrischen Optik erwartet man unabhängig von der Dispersion eine unendlich hohe Auflösung, tatsächlich aber begrenzt auch hier die Beugung das Auflösungsvermögen. Einen Begriff von der Grösse des spektralen Auflösungsvermögens liefert die Betrachtung von Prismen der Basislänge b = 1 cm aus Flintglas und Kronglas. Flintglas hat im optischen Bereich eine Dispersion von 1730 cm ^{- 1}, Kronglas von 530 cm ^{- 1}. Die beiden D-Linien des Natriums (l₁ = 589,5932 nm, l₂ = 588,9965 nm) lassen sich demnach nur mit dem Flintglasprisma trennen.

3) Photographisches Auflösungsvermögen

In der Photographie ist das Auflösungsvermögen ein Mass für die Fähigkeit einer photographischen Schicht, kleine Details erkennbar wiederzugeben. Es wird meist durch die Zahl der Linien pro Millimeter eines Rasters angegeben, welches im Bild eben noch erkannt werden kann. Das Auflösungsvermögen ist von Art und Kontrast des Rasters, der Wellenlänge der Strahlung, der Belichtung, der Entwicklung und vor allem von der Beschaffenheit der photographischen Schicht abhängig. Das Auflösungsvermögen wird begrenzt durch die Kontrastverminderung, durch den Diffusionslichthof und die Körnigkeit. Bei einem Strichraster mit hohem Kontrast misst man etwa 80 Linien/mm bei grobkörnigen und 150-200 Linien/mm bei feinkörnigen Schichten. Bei sehr feinkörnigen und sehr unempfindlichen Schichten sind Werte von mehr als 1000 Linien/mm erreichbar.

4) Auflösungsvermögen des Auges

Das Auflösungsvermögen des Auges ist ein Mass für die Fähigkeit des Auges, räumlich und zeitlich benachbarte Reize zu trennen. Das räumliche Auflösungsvermögen ist über den Winkelabstand Dj definiert, den zwei Objektpunkte bezüglich der Pupillenmitte voneinander haben müssen, um zwei getrennte Lichtempfindungen hervorzurufen. Es wird begrenzt durch die Beugung des Lichtes am Pupillenrand und die endliche Grösse der Zapfen und deren Abstand in der Netzhaut (Beugung). Mit Dj = 1,22 × l/d folgt bei Tageslicht mit einem Pupillendurchmesser d = 3 mm und einer Wellenlänge von l = 550 nm eine Auflösungsgrenze von Dj = 48 ²  (zum Faktor 1,22 Beugung). Aufgrund seines Aufbaus sieht das menschliche Auge zwei Punkte nur dann getrennt, wenn sie unter einem Winkel von Dj > 1 erscheinen (bei einem Abstand von 25 cm müssten die beiden Punkte mindestens 0,04 mm voneinander entfernt sein). Auf der Netzhaut hat das Beugungsscheibchen einen Radius von ca. 6 mm, was dem mittleren Abstand zweier Zapfen in der Netzhaut entspricht, d.h. das Auflösungsvermögen des Auges wird durch die Anordnung der Zapfen in der Netzhaut voll ausgeschöpft. Die Bestimmung des Auflösungsvermögens erfolgt mit Hilfe eines Landolt-Ringes oder verschieden grosser Sehzeichen in konstantem Abstand.

Der kleinste zeitliche Abstand zweier am gleichen Ort aufeinanderfolgender Reize, die zu getrennten Empfindungen führen, bestimmt die zeitliche Auflösungsgrenze, die beim Tagessehen 50 Hz (stroboskopischer Effekt) und beim Dämmerungssehen 10 Hz beträgt. [KB2, MG2]

Auflösungsvermögen: Zur Erklärung der Auflösung zweier Objektpunkte im Bild eines Teleskops.