Techniklexikon

Bindungsenergie

Differenz zwischen der Gesamtenergie E(S) eines in Teilsysteme S_i zerlegbaren Systems S und der Summe der Gesamtenergien E(S_i) der isolierten Teilsysteme S_i:

E_B = E(S) - S_iE(S_i).

Die Bindungsenergie wird also auf die Energie der getrennten ("unendlich voneinander entfernten") Systeme bezogen und hängt daher von der Wahl der Zerlegung des Systems S in die Teilsysteme S_i und deren Zustand ab. Setzt man die Energie des Zustandes des zerlegten Systems auf Null, ist die Bindungsenergie negativ, sofern das System gebunden ist, entsprechend der Tatsache, dass bei dessen Bildung Energie frei wird. Je grösser der Absolutbetrag der Bindungsenergie ist, desto fester ist die Bindung bzw. desto grösser die Bindungsstärke. Wichtige Spezialfälle sind die folgenden:

1) Atomphysik: Die Bindungsenergien von Elektronen in Atomen, Molekülen und Festkörpern liegen im Bereich von wenigen eV für die Leitungselektronen in den Alkalimetallen bis über 100 keV für die am stärksten gebundenen Rumpfelektronen in den schwersten Atomen. Die der berechneten Bindungsenergie entsprechende experimentelle Grösse ist das (negative) Ionisierungspotential. Die Bindungsenergie der Leitungselektronen in Metallen wird auch als Austrittsarbeit bezeichnet.

2) Kernphysik: die Energie, die erforderlich ist, um einen Kern in die einzelnen Nukleonen zu zerlegen. Die Bindungsenergie entspricht dem Energieäquivalent der Differenz zwischen der tatsächlichen Kernmasse und der Summe der Massen aller Protonen und Neutronen, auch als Massendefekt bezeichnet:

,

wobei m_H die Masse eines neutralen Wasserstoffatoms, m_n die Masse des Neutrons, m(Z,N) die Masse des betreffenden Atoms und c die Lichtgeschwindigkeit ist.

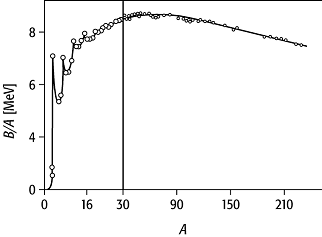
Interessante Folgerungen ergeben sich aus der Betrachtung der Bindungsenergie pro Nukleon B/A, die der mittleren Energie entspricht, die aufgebracht werden muss, um ein einziges Nukleon vom Kern zu separieren (Abb. 1). Für leichte Kerne zeigt B/A erhebliche Schwankungen. So hat das Deuteron mit 1,11 MeV eine besonders niedrige und der Helium-Kern (Alpha-Teilchen) mit 7 MeV eine besonders hohe Bindungsenergie. Im Bereich der leichten Kerne sind die Bindungsenergien für , , ,  und  besonders gross. Jede dieser gg-Kerne enthält eine gleiche Zahl jeweils gepaarter Protonen und Neutronen.

Für grössere A nimmt B/A einen mittleren Wert zwischen 7,5 und 8,5 MeV an, der den Sättigungscharakter der Kernkräfte, also die Tatsache, dass jedes Nukleon nur mit einer beschränkten Anzahl benachbarter Nukleonen wechselwirkt, widerspiegelt (Absättigung).

Da B/A bei A » 56, d.h. im Gebiet um Eisen, ein Maximum mit 8,8 MeV hat, lässt sich sowohl durch Verschmelzen leichter Kerne (Fusion) als auch durch Spaltung schwerer Kerne Energie gewinnen. In beiden Fällen wird Bindungsenergie frei.

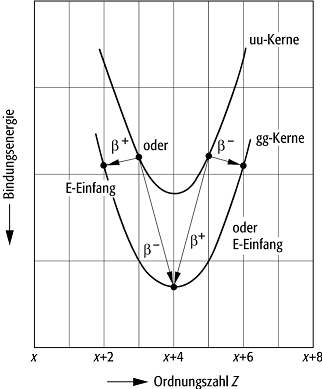
Zur Beschreibung der Abhängigkeit des Massendefekts bzw. der Bindungsenergie der Kerne von der Massenzahl wurden einige semiempirische Formeln entwickelt, deren beste die im Rahmen des Tröpfchenmodells entwickelte Bethe-Weizsäcker-Formel ist. Die Bindungsenergien der Kerne unterscheiden sich für gg-, gu-, ug- und uu-Kerne. Abb. 2 zeigt den Verlauf für uu- und gg-Kerne bei konstantem A, d.h. für Isobare. Wegen des halbzahligen Spins der Nukleonen wird ein paariges Proton oder Neutron fester gebunden als ein unpaariges. Daher ist die Bindungsenergie der gg-Kerne grösser als die der uu-Kerne. Im gezeigten Beispiel existieren drei stabile gg-Kerne und kein stabiler uu-Kern. Die instabilen Kerne zeigen b ^- -Zerfall (Elektronenemission b ^-  und Positronenemission b bzw. Elektronen- oder e ^- -Einfang). Solche Betrachtungen der Bindungsenergien der Kerne führen zu den Isobarenregeln. Das Tal der Energiefläche (Energietal) verläuft wellenförmig. Die Abweichungen vom ausgeglichenen mittleren Verlauf treten an den magischen Zahlen auf; ihre Entdeckung trug zur Entwicklung des Schalenmodells der Kerne bei.

3) Molekülphysik, physikalische Chemie: Die Bindungsenergien typischer kovalenter und ionischer Bindungen (chemische Bindung) in Molekülen liegen im Bereich von knapp 2 (F₂) bis etwa 11 eV (CO), während die Bindungsenergien zwischenmolekularer Wechselwirkungen um etwa eine Grössenordnung kleiner sind. Die theoretisch bestimmte Bindungsenergie D_e eines zweiatomigen Moleküls ist die Differenz der Gesamtenergie des Moleküls im Minimum der Potentialkurve und der Gesamtenergie der getrennten Atome im elektronischen Grundzustand. Nach der Heisenbergschen Unschärferelation kann sich jedoch das Molekül selbst am absoluten Nullpunkt nie im Minimum der Potentialkurve befinden, sondern allenfalls im Schwingungsgrundzustand. Die berechneten Bindungsenergien sind daher nicht direkt mit den gemessenen Dissoziationsenergien D₀ zu vergleichen, sondern müssen um die Nullpunktsenergie E_NP =  ô D_e ô  - D₀ korrigiert werden, die etwa 3 - 6% der Bindungsenergie ausmacht. Die Bindungsenergie mehratomiger Moleküle wird auch als Atomisierungsenergie bezeichnet und entspricht der vollständigen Zerlegung des Moleküls in seine atomaren Bestandteile. Davon zu unterscheiden ist die Bindungsdissoziationsenergie (BDE) oder Trennungsenergie, die den Energiebetrag angibt, der für die Spaltung eines Moleküls in zwei (in ihren Grundzuständen befindliche) Fragmente erforderlich ist. Die folgende Tabelle gibt eine Zusammenstellung der verschiedenen Energien (in kcal/mol) für die Serie CH_n an.

	De	ENP	D0	BDE	D0/n
CH4	419,8	27,7	392,1	103,3	98,0
CH3	307,3	18,6	288,7	108,8	96,2
CH2	190,4	10,5	179,9	100,0	90,0
CH	83,9	4,0	79,9	79,9	79,9

 

Beispielsweise beträgt in CH₄ die mittlere Energie D₀/n einer C-H-Bindung 98,0 kcal/mol, während für die Abspaltung eines H-Atoms gemäss CH₄  CH₃ + H 103,3 kcal/mol erforderlich sind. Der Unterschied ist sowohl geometrisch bedingt (das CH₃-Fragment in CH₄ ist trigonal pyramidal, während das CH₃ Molekül trigonal planar ist) als auch elektronisch (die C-Atome unterscheiden sich in beiden Molekülen hinsichtlich Hybridisierung und effektiver Ladungen). Solche Umordnungseffekte innerhalb der Fragmente können erheblich sein, wie die Bindungsdissoziationsenergien (in kcal/mol) einiger C-Br-Bindungen zeigen:

Name	Formel	BDE(C-Br)
Brombenzol	C6 H5 Br	71
Bromethan	C2 H5 Br	65
Benzylbromid	C6 H5 CH2Br	51
Allylbromid	C3 H5 Br	46

 

Die Berechnung von Atomisierungsenergien durch Summierung von mittleren Bindungsdissoziationsenergien (Bindungsinkremente) der einzelnen Bindungen liefert daher allenfalls qualitative Abschätzungen.

Die Genauigkeit experimentell bestimmter Bindungsenergien für kleine Moleküle (ca. 10 - 15 Atome) liegt im Bereich von 2 kcal/mol, während eine theoretische Berechnung mit den zur Zeit besten Methoden auf 3 - 4 kcal/mol genau möglich ist. Beim Vergleich berechneter Bindungsenergien mit thermochemisch bestimmten Standardbildungsenthalpien (Bildungswärme) sind daher neben der Nullpunktsenergie auch temperaturabhängige Korrekturen zu berücksichtigen [HG1, MG1]

Bindungsenergie 1: Bindungsenergie pro Nukleon als Funktion der Massenzahl A für stabile Kerne. Zur besseren Übersicht ist die Abszisse bis A = 30 gespreizt dargestellt.

Bindungsenergie 2: Schema der Bindungsenergie von Isobaren gerader Massenzahl.