Techniklexikon

fast-integrable Systeme

Nichtlineare Dynamik, Chaos, Fraktale, Hamilton-Systeme, die durch eine Störung eines integrablen Systems entstehen. Während integrable und stark-chaotische Systeme extreme Ausnahmefälle darstellen, die manchmal exakt behandelt werden können, stellen fast-integrable Systeme den typischen oder generischen Fall dar. Sie können in vielen Aspekten nur qualitativ oder numerisch behandelt werden. Das Charakteristikum dieser Systeme ist die Koexistenz regulären und chaotischen Verhaltens im Phasenraum oder auf der Energiefläche konservativer Systeme.

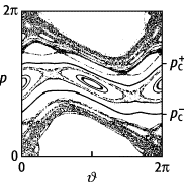
Die einfachsten fast-integrablen Systeme sind solche mit zwei Freiheitsgraden, also vierdimensionalem Phasenraum H = H(q₁, q₂, p₁, p₂), oder getriebene Systeme mit einem Freiheitsgrad H = H(q, p, t) (3 / 2 Freiheitsgrade). Für letztere können, wenn der Antrieb zeitlich periodisch ist, die typischen Phasenraum-Strukturen sehr leicht veranschaulicht werden, indem man Koordinate q(t) und Impuls p(t) nur zu Zeiten, die Vielfache der Periode T sind, in der q-p-Ebene markiert (q_n, p_n) = ( q(t = nT), p(t = nT) ), n = 0, 1, 2,... (stroboskopische Abbildung, Wiederkehrabbildung). Für ein viel untersuchtes System, den periodisch angestossenen Rotator , sind in der Abb. Phasenraumstrukturen dargestellt, die man für verschiedene Anfangsbedingungen (q₀, p₀) erhält. Die linienartigen, regulären Strukturen sind einerseits deformierte Überreste des integrablen Verhaltens für k = 0 (Linien bei  und ). Die Existenz dieser topologisch kreisförmigen Gebilde (1-d-Tori, J = Winkel) wird für kleine k durch das Kolmogorow-Arnold-Moser-Theorem (KAM-Theorem) garantiert. Andererseits findet man ellipsenartige Linien (elliptische Inseln, die sich in der Nähe stabiler, periodischer Trajektorien befinden. Ihre Existenz ist die Folge einer Resonanz von Antriebsfrequenz und einer internen, natürlichen Systemfrequenz und wird formell durch das Poincaré-Birkhoff-Theorem erklärt. Zwischen den elliptischen Inseln, in der Nähe instabiler, periodischer Trajektorien, zeigen Iterationen (q_n, p_n) chaotisches Verhalten, was sich unter anderem in der flächenhaften Verteilung dieser Punkte niederschlägt (chaotischer See). Bei höherer räumlicher Auflösung findet man innerhalb der elliptischen Inseln auf einer sehr viel kleineren Skala auch noch chaotische Seen, die wiederum noch kleinere elliptische Inseln besitzen, usw., also eine unendliche Hierarchie von chaotischen und regulären Strukturen. Ein qualitativ ähnliches Verhalten findet man im Poincaré-Schnitt einer Energiefläche eines Systems mit zwei Freiheitsgraden. Auch hier sind die in den chaotischen See eingebetteten elliptischen Inseln und die regulären KAM-Linien für chaotische Trajektorien undurchlässig. In Systemen mit mehr als zwei Freiheitsgraden bilden die regulären Strukturen keine absoluten Barrieren mehr, ein chaotischer Orbit kann dann z.B. in das Innere einer elliptischen Insel hinein diffundieren (Arnold-Diffusion). [GR2]

fast-integrable Systeme: Phasenraumstrukturen des periodisch angestossenen Rotators (für k » 0,97, T = 1), wie man sie in den typischen fast-integrablen Systemen mit 1 1 / 2 oder zwei Freiheitsgraden findet. Gezeigt sind je 5000 Iterationen der entsprechenden Wiederkehrabbildung von 13 verschiedenen Anfangsbedingungen. Die weissen Flächen sind entweder ebenfalls mit elliptischen Inseln besetzt oder durch KAM-Linien von den chaotischen Komponenten abgetrennt.