Techniklexikon

Lebesgue-Integral

eine Verallgemeinerung des Riemann-Integrals, die die Integration einer wesentlich umfangreicheren Klasse von Funktionen erlaubt. Das Lebesgue-Integral einer im Intervall  beschränkten Funktion  beruht auf der Lebesgue-Summe

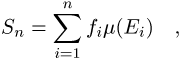
wobei n die Zahl der Teilintervalle, f_i den Wert der Funktion im Teilintervall i bezeichnet und m das Lebesgue-Mass der Menge E_i von Punkten ist, deren Funktionswert approximativ durch f_i gegeben ist. Konvergieren die Längen der Teilintervalle gleichmässig gegen Null, so existiert der  und gibt den Wert des Lebesgue-Integrals von f auf I an. Da jede abzählbare Menge im Lebesgueschen Sinne eine Nullmenge ist, kann die Funktion f auf einer abzählbaren oder jeder anderen Nullmenge abgeändert werden, ohne dass sich der Wert des Lebesgue-Integrals ändert.