Techniklexikon

Markow-ProzessNichtlineare Dynamik, Chaos, Fraktale

von A.A. Markow erstmals genauer untersuchter, zufälliger Prozess, bei dem die zukünftige Entwicklung vollständig durch den gegenwärtigen Zustand bestimmt ist und nicht vom Verhalten in der Vergangenheit abhängt. Für einen in diskreten Zeitschritten erfolgenden Prozess (Markow-Kette) ist also die Übergangswahrscheinlichkeit  vom Zustand  zur Zeit m zum Zustand  zur Zeit m + 1 nur eine Funktion von i und j. Die Wahrscheinlichkeit dafür, beginnend in i den Zustand j nach n Schritten zu erreichen, kann dann in Form eines über Zwischenzustände k verlaufenden Prozesses angegeben werden (Chapman-Kolmogorow-Gleichung),

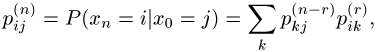
woraus sich für die numerische Berechnung günstige Formeln ableiten lassen. (stochastische Prozesse)