Techniklexikon

Airysche Differentialgleichung

die Differentialgleichung y ²  - xy = 0, die z.B. die stationären Zustände einer quantenmechanischen Wellenfunktion in einem Potential beschreibt, welches proportional zu x anwächst. Lösungen dieser Gleichung sind die Linearkombinationen der Airyschen Funktionen Ai(x) und Bi(x). Diese lassen sich durch die Linearkombinationen  und  der beiden schnell konvergierenden Potenzreihen

 und

definieren, der Konvergenzradius ist unendlich. Die Linearkombinationen für Ai und Bi sind dabei so gewählt, dass für x  ¥  Bi(x) exponentiell anwächst, während Ai(x) exponentiell abfällt, und für x   - ¥  beide um 90° phasenverschoben oszillieren, und zwar mit anwachsender Wellenzahl und abnehmender Amplitude. Die Airysche Differentialgleichung kann auch als Bewegungsgleichung für ein Federpendel aufgefasst werden, dessen Federkonstante proportional zur Zeit abfällt.

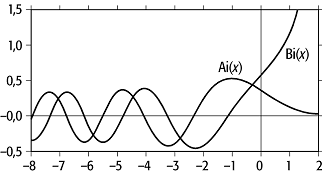
Airysche Differentialgleichung: Verlauf der Airyschen Funktionen