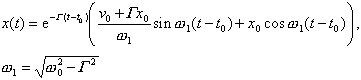Techniklexikon

Differentialgleichung

Mathematische Methoden und Computereinsatz, mathematische Gleichung, die Ableitungen einer unbekannten Funktion y enthält. Differentialgleichungen spielen in der Physik eine überragende Rolle, da physikalische Gesetze und Zusammenhänge sich häufig als Differentialgleichung darstellen lassen.

Begriffe und Schreibweisen:

Jede Funktion, welche eine gegebene Differentialgleichung erfüllt, heisst Lösung dieser Differentialgleichung, in der Regel gibt es davon unendlich viele. Das Lösen einer Differentialgleichung besteht darin, alle Lösungen zu finden. Stellt man an die Funktion y oder ihre Ableitungen in bestimmten Punkten gewisse Bedingungen, so lässt sich die Lösungsmenge einschränken. Beziehen sich diese Bedingungen auf einen bestimmten Zeitpunkt t₀ und ist man am Verhalten y(t) der Funktion für t > t₀ interessiert, nennt man sie Anfangsbedingungen. Gibt man Funktionswerte auf dem Rand eines räumlichen Gebietes vor und ist am Verhalten der Funktion im Gebiet interessiert, spricht man dagegen von Randbedingungen. Bei Differentialgleichungen, die sowohl Orts- als auch Zeitableitungen enthalten, kommen auch kombinierte Anfangs- und Randbedingungen vor. Anfangswertprobleme, d.h. Differentialgleichungen zusammen mit Anfangsbedingungen, sind unter ziemlich allgemeinen Voraussetzungen eindeutig lösbar, während bei reinen Randwertproblemen die Lage verwickelter ist.

Die Ordnung einer Differentialgleichung ist die höchste Ordnung der Ableitungen, die in ihr vorkommen. Die meisten Differentialgleichungen in der Physik sind von der Ordnung eins oder zwei. Lineare Differentialgleichungen haben die Form L[y(x)] = R(x), wobei L ein linearer Differentialoperator und R eine reellwertige Funktion ist. Viele wichtige Differentialgleichungen in der Physik sind linear. Nichtlineare Differentialgleichungen können entweder linearisiert, d.h. durch eine lineare Differentialgleichung angenähert bzw. durch eine geeignete Transformation in eine lineare Differentialgleichung überführt werden, oder sie führen zu Phänomenen wie Bifurkation, Katastrophe, Hysterese und Chaos. Gewöhnliche Differentialgleichungen sind solche, in denen nur Ableitungen nach einer Veränderlichen vorkommen, während partielle Differentialgleichungen Ableitungen der unbekannten Funktion nach mehreren Variablen enthalten. Wichtige Beispiele gewöhnlicher Differentialgleichungen in der Physik sind die Bewegungsgleichungen, die nur zeitliche Ableitungen enthalten, z.B. die Newtonsche Bewegungsgleichung und die Schwingungsgleichung, und darüber hinaus solche Gleichungen, die als Zwischenschritte bei der Lösung partieller Differentialgleichungen auftreten, z.B. die Besselsche und die Legendresche Differentialgleichung. Partielle Differentialgleichungen sind z.B. die Schrödinger-Gleichung, die Maxwell-Gleichungen, die Wellengleichung, die Poisson-Gleichung, die Laplace-Gleichung und die Diffusionsgleichung. Sie enthalten räumliche Ableitungen nach den drei Ortskoordinaten und teilweise auch zeitliche Ableitungen.

In Differentialgleichungen wird die erste, zweite und n-te Ableitung einer Funktion y nach einer Variablen x als dy/dx, d²y/dx² und dⁿy/dxⁿ, als y/x, ²y/x² und ⁿy/xⁿ, als  oder als y_x, y_xx, y_xxx usw. geschrieben, wobei das Symbol " anstelle von "d" insbesondere bei partiellen Differentialgleichungen verwendet wird. Bei gewöhnlichen Differentialgleichungen verwendet man auch die Schreibweisen y ¢ , y ²  und y⁽ⁿ⁾, da hier Verwechslungen der Variablen ausgeschlossen sind. In Bewegungsgleichungen werden erste und zweite Zeitableitungen auch als  und  bezeichnet; die Verwendung höherer als zweiter Zeitableitungen bringt für physikalische Probleme in der Regel keinen Nutzen. In partiellen Differentialgleichungen kommt häufig der Laplace-Operator D vor, der in kartesischen Koordinaten (x, y, z) die Darstellung  besitzt.

Bewegungsgleichungen:

Die Zeitentwicklung eines Systems beschreibt man durch Bewegungsgleichungen, bei denen es sich um gewöhnliche Differentialgleichungen erster oder zweiter Ordnung in der Zeit handelt. Zusammen mit Anfangsbedingungen (der Funktionswert und im Falle einer Differentialgleichung zweiter Ordnung auch die Zeitableitung des Funktionswertes zu einem Anfangszeitpunkt) sind solche Gleichungen eindeutig lösbar. Die Bewegungsgleichung dx/dt = kx beschreibt Situationen, in denen die Änderungsrate einer Grösse proportional zur Grösse selbst ist. Gewöhnliche Differentialgleichungen erster Ordnung, die separabel sind, d.h. sich in der Form dx/dt = P(t)/Q(x) schreiben lassen, können durch Integration gelöst werden: . In der obigen Gleichung ist P(t) = 1 und Q(x) = 1/x, daher ist x = x₀ exp (k(t - t₀)) die Lösung unter der Anfangsbedingung x(t₀) = x₀. Im Falle von k > 0 beschreibt dies ein exponentielles Wachstum, bei k < 0 ein exponentielles Abklingen. Für die Lösung der Differentialgleichung dx/dt + tx = 0 mit der Anfangsbedingung x(0) = 1 erhält man in analoger Weise die Gauss-Funktion x = exp( - t²/2). Gleichungen, die nicht separabel sind, lassen sich manchmal durch Substitution auf separable Gleichungen zurückführen. In ihrer allgemeinsten Form dx/dt = f(t, x) lassen sich gewöhnliche Differentialgleichungen erster Ordnung zwar nicht analytisch lösen, aber man kann zu numerischen Verfahren greifen. Sehr intuitiv ist die Euler-Methode, die aber nicht besonders genau und stabil ist. Hier wird der Differentialquotient einfach durch den Differenzenquotient ersetzt. Besser sind Mehrschrittverfahren, z.B. das Adams-Bashforth- oder das Adams-Moulton-Verfahren, bzw. Prediktor-Korrektor-Algorithmen. Am häufigsten verwendet man jedoch die Runge-Kutta-Methoden.

Diese numerischen Methoden lassen sich auch auf Systeme von Differentialgleichungen erster Ordnung verallgemeinern. Solche Systeme, die auch als gekoppelte Differentialgleichungen bezeichnet werden, lassen sich in der Form  schreiben, wobei x ein Vektor ist, und sind eine ziemlich allgemeine Klasse von Gleichungen. Dies rührt daher, dass sich Systeme gewöhnlicher Differentialgleichungen höherer Ordnung in einfacher Weise durch Substitution aller Ableitungen durch neue Variable auf ein Differentialgleichungssystem erster Ordnung zurückführen lassen. Die kanonischen Gleichungen

, , i = 1, . . . , N

der analytischen Mechanik bilden ein System von 2N gewöhnlichen Differentialgleichungen erster Ordnung. Einen wichtigen Sonderfall, den man auch analytisch lösen kann, stellen Systeme homogener linearer Differentialgleichungen erster Ordnung mit konstanten Koeffizienten dar, welche die allgemeine Form  besitzen, wobei x ein Vektor und A eine Matrix ist. Wenn A nicht entartet ist, d.h. wenn die Eigenwerte l_i von A alle verschieden sind, lautet die Lösung , wobei die a_i die Eigenvektoren zu den Eigenwerten l_i sind und sich die Konstanten c_i aus den Anfangsbedingungen x₀ = x(t₀) ergeben. Ein solches Differentialgleichungssystem sind z.B. die kanonischen Gleichungen gekoppelter Oszillatoren. Systeme linearer Differentialgleichungen mit konstanten Koeffzienten lassen sich oft sehr elegant mit Hilfe der Laplace-Transformation lösen; dies gilt auch dann, wenn sie inhomogen sind.

Differentialgleichung 1: Lösungen einiger eindimensionaler Bewegungsgleichungen.

Physikalisches Problem	Bewegungsgleichung	Lösung (unter den Anfangsbedingungen x(t0) = x0 und gegebenenfalls
Exponentielles Wachstum	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'>	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'>
Exponentielles Abklingen	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'>	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'>
Kräftefreie Bewegung	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'>	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'>
Freier Fall	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'>	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'>
Freie Schwingung	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'>	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'>
Gedämpfte Schwingung	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'>	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'>

 

Lineare Differentialgleichungen:

Viele Differentialgleichungen der Physik sind linear. Lineare Differentialgleichungen (LDGln) lassen sich als  schreiben, wobei L ein linearer Differentialoperator ist. Sie können sowohl partielle als auch gewöhnliche Differentialgleichungen und sogar Systeme von Differentialgleichungen sein, und die meisten der Aussagen in diesem Abschnitt gelten für alle diese Fälle. Eine LDGl heisst homogen, wenn R(x) = 0, anderenfalls inhomogen. Die Inhomogenität R(x) wird häufig auch als Störung bzw. Störfunktion bezeichnet. Aus der Linearitätseigenschaft L[ay₁ + by₂] = aL[y₁] + bL[y₂], wobei a, b beliebige Konstanten und y₁, y₂ beliebige Funktionen sind, folgen die nachstehenden Superpositionssätze:

a) Sind y₁ und y₂ Lösungen einer homogenen LDGl, dann ist für beliebige Konstanten c₁ und c₂ der Ausdruck c₁y₁ + c₂y₂ ebenfalls eine Lösung.

b) Ist y_i eine Lösung einer inhomogenen LDGl und y_h eine Lösung der zugehörigen homogenen LDGl, d.h. zur Gleichung, die man aus der ursprünglichen inhomogenen Gleichung erhält, indem man die rechte Seite null setzt, dann ist auch y_i + y_h eine Lösung der inhomogenen LDGl.

Die Lösungen einer homogenen LDGl bilden einen Vektorraum. Bei gewöhnlichen Differentialgleichungen ist dessen Dimension gleich der Ordnung der Differentialgleichung, bei partiellen Differentialgleichungen ist er im allgemeinen unendlichdimensional. Eine Basis dieses Vektorraumes heisst Fundamentalsystem von Lösungen der Differentialgleichung. Die Funktionen y₁ = sin(wt) und y₂ = cos(wt) bilden ein Fundamentalsystem von Lösungen der Schwingungsgleichung . Kennt man ein Fundamentalsystem y₁, . . . , y_n, so lassen sich die allgemeine Lösung einer homogenen LDGl in der Form  schreiben; die allgemeine Lösung der Schwingungsgleichung lautet y(t) = A sin(wt) + B cos(wt) mit beliebigen Konstanten A und B. Inhomogene gewöhnliche LDGln lassen sich ebenfalls mit dem Ansatz  lösen, wenn die Koeffizienten a_i als variabel aufgefasst werden. Dieses Verfahren nennt man Variation der Konstanten. Zur Gleichung , die eine ungedämpfte erzwungene Schwingung mit Eigenfrequenz w₀ und Anregungsfrequenz w beschreibt, findet man auf diese Weise die Lösung

.

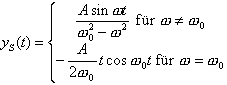Dabei handelt es sich jedoch nur um eine spezielle oder partikuläre Lösung dieser inhomogenen LDGl; die allgemeine Lösung y(t) lässt sich als Summe einer solchen speziellen Lösung und der allgemeinen Lösung der zugehörigen homogenen LDGl schreiben: y(t) = y_S(t) + B sin (w₀t) + C cos (w₀t). Anfangsbedingungen y(t₀) = y₀ und y ¢ (t₀) = v₀ führen schliesslich auf ein lineares Gleichungssystem für die Koeffizienten B und C, das wegen des Nichtverschwindens der Wronski-Determinante  eindeutig lösbar ist. Im Falle von Randbedingungen kann das entstehende Gleichungssystem hingegen eine, keine oder unendlich viele Lösungen besitzen. Eine andere Methode zur Lösung inhomogener LDGln, die insbesondere bei Randwertproblemen partieller LDGln häufig angewendet wird, ist die Verwendung von Green-Funktionen. Eine Funktion G(x,x ¢ ) heisst Green-Funktion zu einem linearen Differentialoperator L, wenn L[G(x,x ¢ )] = d(x - x ¢ ) gilt. In diesem Fall ist  eine Lösung der LDGl L[y(x)] = f(x), wie man unmittelbar durch Einsetzen verifizieren kann. Kennt man also eine Green-Funktion, kann man zu inhomogenen LDGln für beliebige Störfunktionen f (x) durch direkte Integration eine Lösung finden. Dieses Prinzip lässt sich auf Probleme mit homogenen Randbedingungen ausdehnen, d.h. solche Randbedingungen, die durch y º 0 erfüllt werden. Kennt man nämlich eine Green-Funktion, die in x solchen Randbedingungen genügt, dann werden diese auch von y_G(x) erfüllt. Die Green-Funktion des Laplace-Operators, die der Randbedingung G(r,r ¢ )  0 für r   ¥  genügt, ist G(r, r ¢ ) =  - (4p ô r - r ¢  ô ) ^{- 1}. DDemnach lautet die Lösung der Poisson- Gleichung DF(r) =  - 4pr(r) unter denselben Randbedingungen  .

Lineare partielle Differentialgleichungen zweiter Ordnung:

Lineare partielle Differentialgleichungen, in denen Ort und Zeit als Variable auftreten, gehören zu den wichtigsten Differentialgleichungen der Physik (Tabelle 2). Alle in der Tabelle aufgeführten Gleichungen sind von zweiter Ordnung in den Ortskoordinaten, wobei die Ortsableitungen stets durch den Laplace-Operator gegeben werden. Nicht aufgeführt sind die Maxwell-Gleichungen, bei denen es sich um ein System partieller Differentialgleichungen erster Ordnung handelt, die aber durch die Einführung von Potentialen in inhomogene Wellengleichungen für das skalare Potential und das Vektorpotential umgeformt werden können. Die linearen partiellen Differentialgleichungen zweiter Ordnung werden in drei Klassen eingeteilt: elliptische Differentialgleichungen (z.B. Laplace-Gleichung), parabolische Differentialgleichungen (z.B. Diffusionsgleichung): hyperbolische Differentialgleichungen (z.B. Wellengleichung). Elliptische Differentialgleichungen sind eindeutig lösbar, wenn die Funktionswerte auf dem Rand eines Gebietes vorgegeben werden (Dirichletsche Randbedingungen). Werden stattdessen die Normalableitungen auf dem Rand des Gebietes vorgegeben (Neumannsche Randbedingungen), ist die Lösung nur bis auf eine additive Konstante eindeutig bestimmt. Im Falle parabolischer und hyperbolischer Differentialgleichungen benötigt man für eine eindeutige Lösung neben Dirichletschen oder Neumannschen Randbedingungen noch Anfangsbedingungen F(r,t₀) und gegebenenfalls auch ¶F/¶t zu einem Zeitpunkt t = t₀.

Differentialgleichung 2: Partielle Differentialgleichungen der Physik.

bottom:none;mso-border-top-alt:solid black .75pt;mso-border-left-alt: solid black .75pt;mso-border-right-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'> Gleichung	bottom:none;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-top-alt:solid black .75pt; mso-border-left-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'> Name	bottom:none;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-top-alt:solid black .75pt; mso-border-left-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'> Physikalischer Ursprung
bottom:none;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'>	Laplace-Gleichung	Elektrostatik, Magnetostatik, stationäre Wärmeleitung ohne Quellen
bottom:none;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'>	Poisson-Gleichung	Elektrostatik, Magnetostatik, stationäre Wärmeleitung mit Quellen
bottom:none;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'>	Helmholtz-Gleichung	Eigenschwingungen und Eigenmoden
bottom:none;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'>	stationäre Schrödinger-Gleichung	stationäre Zustände in der Quantenmechanik
bottom:none;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'>	Diffusionsgleichung	Diffusion, Wärmeleitung, Transport
bottom:none;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'>	zeitabhängige Schrödinger- Gleichung	Quantenmechanik
bottom:none;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'>	Navier-Stokes-Gleichung	inkompressible Flüssigkeiten
bottom:none;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'>	Wellengleichung	Freie Wellen
bottom:none;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'>	inhomogene Wellengleichung	angeregte Wellen
bottom:none;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'>	Klein-Gordon-Gleichung	Wellen mit Dispersion, relativistische Quantenmechanik
bottom-alt: solid black .75pt;mso-border-right-alt:solid black .75pt;padding:0cm 0cm 0cm 0cm\'>	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-bottom-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'> Telegraphengleichung	bottom:solid black 1.0pt;border-right:solid black 1.0pt; mso-border-left-alt:solid black .75pt;mso-border-left-alt:solid black .75pt; mso-border-bottom-alt:solid black .75pt;mso-border-right-alt:solid black .75pt; padding:0cm 0cm 0cm 0cm\'> gedämpfte Wellen

 

Partielle Differentialgleichungen formuliert man am besten in solchen Ortskoordinaten, die zu den Randbedingungen passen, d.h. in denen die Randbedingungen eine möglichst einfache Form besitzen. Hierzu benötigt man insbesondere die verschiedenen Formen des Laplace-Operators in den einzelnen Koordinatensystemen. Kartesische Koordinaten (x, y, z) sind geeignet, wenn die Funktionswerte auf dem Rand eines rechteckigen oder quaderförmigen Gebietes vorgegeben sind, also z.B. für die Eigenschwingungen einer rechteckigen Membran oder die elektromagnetischen Eigenmoden eines kastenförmigen Hohlraumes. Zylinderkoordinaten (r, f, z) eignen sich eher für die Lösung der Navier-Stokes-Gleichung in einem zylindrischen Rohr oder für die Bestimmung der Eigenmoden eines Hohlleiters. Für die häufig anzutreffende Randbedingung F(r)  0 für  ô r ô ¥  verwendet man am besten Kugelkoordinaten (r, q, f).

Zur Lösung partieller Differentialgleichungen kann man eine oder mehrere der folgenden Strategien anwenden:

a) Variablentrennung: Hierzu macht man für die Fundamentallösungen der homogenen Gleichung einen Produktansatz der Art F(x,y) = X(x)Y(y). Durch Trennung von Orts- und Zeitvariablen gelangt man beispielsweise von der zeitabhängigen zur stationären Schrödinger-Gleichung: Setzt man y(r,t) = F(r)T(t) für die Lösungen von

an, erhält man nach Einsetzen und Division durch y die Gleichung

.

Da deren linke Seite nur von r und die rechte Seite nur von t abhängt, müssen beide Seiten konstant sein. Bezeichnet man diese Konstante mit E, erhält man für den zeitlichen Teil die Gleichung  und für den räumlichen Teil die stationäre Schrödinger-Gleichung

.

Die ursprüngliche partielle Differentialgleichung mit drei Orts- und einer Zeitkoordinate wurde also in eine partielle Differentialgleichung in den drei Ortskoordinaten und eine gewöhnliche Differentialgleichung in der Zeit überführt, die durch die Trennungskonstante E miteinander gekoppelt sind. Auf analoge Weise gelangt man von der Wellengleichung zur Helmholtz-Gleichung. Durch Trennung nach den Raumkoordinaten kann man in vielen Fällen partielle Differentialgleichungen, die nur vom Ort abhängen, auf drei gewöhnliche Differentialgleichungen zweiter Ordnung zurückführen, die über zwei Trennungskonstanten miteinander verbunden sind. Unter Berücksichtigung der Randbedingungen sind für die Trennungskonstanten in der Regel nur diskrete Werte möglich.

b) Integraltransformation: Unter Fourier-Transformation (ebenso wie unter Laplace-Transformation) werden Ableitungen zu Multiplikationen mit einer Konstanten. Aufgrund dieser Eigenschaft lassen sich Differentialgleichungen in transformierter Form häufig leichter lösen: Partielle Differentialgleichungen werden zu gewöhnlichen Differentialgleichungen, und Systeme gewöhnlicher Differentialgleichungen werden zu algebraischen Gleichungssystemen.

c) Greensche Funktion: Mit Hilfe von Green-Funktionen lassen sich inhomogene Differentialgleichungen mit homogenen Randbedingungen, wie weiter oben bereits beschrieben, durch Integration lösen. Die Probleme bestehen dann darin, inhomogene Randwertaufgaben in homogene Randwertaufgaben zu verwandeln, zu gegebenen Differentialoperatoren und Randbedingungen die Green-Funktion zu finden und schliesslich das resultierende Integral auszuwerten.

d) Numerische Lösung: Partielle Differentialgleichungen lassen sich mit Computern lösen, indem man den Raum bzw. die Raum-Zeit mit Hilfe eines Gitters diskretisiert. Die Diskretisierung des linearen Differentialoperators ergibt lineare Gleichungen für die Funktionswerte in den Gitterpunkten. In diskretisierter Form ist eine lineare partielle Differentialgleichung folglich ein im allgemeinen sehr grosses und dünn besetztes lineares Gleichungssystem für die Funktionswerte in den Gitterpunkten, dessen rechte Seite durch die Randbedingungen, d.h. die Funktionswerte in den Randpunkten bestimmt wird. Probleme bei der Numerik partieller Differentialgleichungen bestehen darin, geeignete Gitter zu finden, die zu einem stabilen Lösungsverhalten führen, das Gitter an die Form des Randes anzupassen und schliesslich das sich ergebende lineare Gleichungssystem effizient zu lösen (Gauss-Seidel-Verfahren, Methode der konjugierten Gradienten, Mehrgitterverfahren). Die durch die Gitterpunkte und deren Verknüpfungen bewirkte Raumzerlegung bezeichnet man auch als Zerlegung in finite Elemente.

Eigenwert-Differentialgleichungen:

Eigenwert-Differentialgleichungen sind homogene, lineare Differentialgleichungen von der Form L[y] = ly, wobei L ein linearer Differentialoperator ist. Sie können sowohl gewöhnliche als auch partielle Differentialgleichungen sein. Unter gegebenen Randbedingungen gibt es nur für manche Werte von l Lösungen; diese Werte bezeichnet man als Eigenwerte des Differentialoperators L, und die Lösungen zu einem speziellen Eigenwert l nennt man Eigenfunktionen von L zum Eigenwert l. Meist fordert man ausserdem, dass L selbstadjungiert unter einem geeigneten Skalarprodukt (y₁,y₂) ist, d.h. dass für alle Funktionen y₁, y₂ die Beziehung (L[y₁],y₂) = (y₁,L[y₂]) gilt. Zu Eigenwert-Differentialgleichungen mit selbstadjungierten Differentialoperatoren sind alle Eigenwerte reell, und zwar auch dann, wenn die Funktionen y komplexwertig sein dürfen; ausserdem sind Eigenfunktionen y_i, y_j zu verschiedenen Eigenwerten l_i, l_j orthogonal, d.h. sie erfüllen (y_i,y_j) = 0 unter demselben Skalarprodukt, unter dem L selbstadjungiert ist. Ist L darüber hinaus ein Differentialoperator zweiter Ordnung, lassen sich die Eigenfunktionen so wählen, dass sie eine vollständige orthogonale Basis des Funktionenraumes unter den entsprechenden Randbedingungen bilden; eine beliebige mit den Randbedingungen verträgliche Funktion z(x) lässt sich dann in der Form  schreiben (Entwicklung nach Eigenfunktionen). Die stationäre Schrödinger-Gleichung Hy = Ey der Quantenmechanik ist eine Eigenwert-Differentialgleichung mit dem Hamilton-Operator H als selbstadjungiertem Differentialoperator zweiter Ordnung. Gewöhnliche Eigenwert-Differentialgleichungen zweiter Ordnung treten in der Physik ausserdem bei der Variablentrennung partieller Differentialgleichungen auf. Diese sind dann zwar im allgemeinen nicht selbstadjungiert, können aber stets durch eine geeignete Transformation in selbstadjungierte Form gebracht werden.

Wichtige gewöhnliche Eigenwert-Differentialgleichungen zweiter Ordnung sind

a) die Legendre-Gleichung  unter der Randbedingung y( ± 1) <  ¥ , deren Eigenfunktionen zu den Eigenwerten l_l =  - l(l + 1) die Legendre-Polynome P_l(x) sind,

b) die zugeordnete Legendre-Gleichung

mit den Eigenwerten l_l =  - l(l + 1) und den Eigenfunktionen

(zugeordnete Legendre-Polynome),

c) die Bessel-Gleichung

unter den Randbedingungen y(0) <  ¥  und y(x)  0 für x   ¥  mit den Eigenwerten l_n = n² und den Eigenfunktionen J_n(x) (Bessel-Funktionen),

d) die sphärische Bessel-Gleichung

mit den Eigenwerten l_n = l(l + 1) und den Eigenfunktionen j_l(x) (sphärische Bessel-Funktionen),

e) die Hermitesche Differentialgleichung

mit den Eigenwerten l_n = 2n und den Eigenfunktionen H_n(x) (Hermite-Polynome),

f) die stationäre Schrödinger-Gleichung

für den eindimensionalen harmonischen Oszillator mit den Eigenwerten E_n = 2n + 1 und den Eigenfunktionen ,

g) die zugeordnete Laguerresche Differentialgleichung

mit den Eigenwerten l_n =  - n und den Eigenfunktionen  (zugeordnete Laguerre-Polynome).

Eigenwert-Differentialgleichungen, deren Eigenwerte und analytische Lösungen nicht bekannt sind, können numerisch durch die Schiessmethode gelöst werden, bei der man für l einen geratenen Wert k verwendet, die Differentialgleichung mit dem geratenen Wert, z.B. mit Hilfe des Numerow-Algorithmus, von einem Randpunkt a beginnend numerisch integriert und prüft, ob die erhaltene Funktion f_k(x) die Randbedingung y(b) = y_b im anderen Randpunkt einhält. Das Problem der Eigenwertbestimmung besteht dann darin, die Nullstellen der Funktion F(k) = f_k(b) - y_b zu finden.  [GB1]