Techniklexikon

Approximation

Annäherung einer Funktion f(x) oder einer Reihe von Messpunkten  durch eine Approximationsfunktion F(x), die einer vorgegebenen Klasse von Funktionen mit n freien Parametern c₁, c₂, ..., c_n angehören soll. Bei der Approximation einer Messreihe, auch als Fit bezeichnet, wendet man üblicherweise die Approximation im quadratischen Mittel an, bei der die c_k so zu bestimmen sind, dass 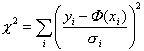minimal wird. Funktionen kann man ebenfalls im quadratischen Mittel approximieren, dabei wäre entsprechend der Ausdruck  zu minimieren; günstiger ist hier jedoch die gleichmässige Approximation, bei der man die c_k so wählt, dass der maximale Approximationsfehler  möglichst klein wird. Im allgemeinen sind beide Arten der Approximation nichtlineare Optimierungsaufgaben der Form . Lässt sich F(x) als Linearkombination  darstellen, dann führt die Approximation im quadratischen Mittel auf ein lineares Gleichungssystem  mit  und . Ein typisches Beispiel ist die Approximation durch Polynome (j_k(x) =  x^{k - 1}) mit dem Spezialfall n = 2, der zur linearen Regression führt. Hat man die beste Approximationsfunktion gefunden, kann man anschliessend mit Hilfe des Chi-Quadrat-Tests beurteilen, ob diese im Hinblick auf die Genauigkeit der Messwerte gut genug ist.