Techniklexikon

Chi-Quadrat-Test

c²-Test, Methode aus der mathematischen Statistik, mit deren Hilfe man beurteilen kann, ob eine Serie von N Messpunkten  mit der Annahme verträglich ist, dass zwischen x und y ein bestimmter funktionaler Zusammenhang y = f(x) besteht. Die Unsicherheiten der x-Werte sollen dabei vernachlässigbar sein. Man definiert c² dann als 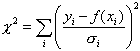und das reduzierte c² als , wobei d die Anzahl der Freiheitsgrade ist, die hier als Anzahl der Messungen abzüglich der Anzahl der aus den Messungen bestimmten Parameter von f(x) definiert ist. Möchte man beispielsweise untersuchen, ob die Messpunkte mit der Annahme eines nicht näher bestimmten linearen Zusammenhanges zwischen x und y verträglich sind, bestimmt man zunächst die Ausgleichsgerade f(x) = ax + b und berechnet anschliessend , wobei d = N - 2 zu verwenden ist, da zwei Parameter, nämlich a und b, aus den Messpunkten bestimmt wurden. Der Erwartungswert für  ist 1. Ist das berechnete  viel grösser als 1, dann sind die Messpunkte nicht mit der Annahme verträglich, ist es dagegen viel kleiner als 1, hat man entweder zuviel in die Messungen hinein interpretiert, d.h. die Kurve f(x) zu genau an die Messpunkte angepasst, oder die Unsicherheiten zu pessimistisch abgeschätzt. Dabei ist zu beachten, dass eine grosse Abweichung des reduzierten c² von 1 um so eher akzeptabel ist, je kleiner die Zahl die Zahl der Freiheitsgrade ist. Präzisere Aussagen über den Grad der Übereinstimmung von Messung und Hypothese erhält man, wenn man die Chi-Quadrat-Verteilung betrachtet, welche die Wahrscheinlichkeitsverteilung des berechneten  angibt unter der Annahme, dass die Messpunkte y_i um die Funktionswerte f(x_i) mit Standardabweichung s_i normalverteilt sind.

 

Chi-Quadrat-Test: Die Chi-Quadrat-Verteilung ist ein Hilfsmittel des Chi-Quadrat-Tests, mit dem man den Grad der Übereinstimmung von Theorie und Experiment beurteilen kann. Die Tabelle enthält die Wahrscheinlichkeiten dafür, bei d Freiheitsgraden Werte für  zu erhalten, die grösser als die in der in der ersten Zeile angegebenen Werte sind.

bottom:1.5pt;border-right:1.5pt;border-color:black;border-style: solid;mso-border-top-alt:.75pt;mso-border-left-alt:.75pt;mso-border-bottom-alt: 1.5pt;mso-border-right-alt:1.5pt;mso-border-color-alt:black;mso-border-style-alt: solid;padding:0cm 3.55pt 0cm 3.55pt\'> d	bottom:solid black 1.5pt;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black 1.5pt; padding:0cm 3.55pt 0cm 3.55pt\'>  0	bottom:solid black 1.5pt;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black 1.5pt; padding:0cm 3.55pt 0cm 3.55pt\'>  0,25	bottom:solid black 1.5pt;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black 1.5pt; padding:0cm 3.55pt 0cm 3.55pt\'>  0,5	bottom:solid black 1.5pt;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black 1.5pt; padding:0cm 3.55pt 0cm 3.55pt\'>  0,75	bottom:solid black 1.5pt;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black 1.5pt; padding:0cm 3.55pt 0cm 3.55pt\'>  1,0	bottom:solid black 1.5pt;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black 1.5pt; padding:0cm 3.55pt 0cm 3.55pt\'>  1,25	bottom:solid black 1.5pt;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black 1.5pt; padding:0cm 3.55pt 0cm 3.55pt\'>  1,5	bottom:solid black 1.5pt;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black 1.5pt; padding:0cm 3.55pt 0cm 3.55pt\'>  1,75	bottom:solid black 1.5pt;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black 1.5pt; padding:0cm 3.55pt 0cm 3.55pt\'>  2	bottom:solid black 1.5pt;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black 1.5pt; padding:0cm 3.55pt 0cm 3.55pt\'>  3	bottom:solid black 1.5pt;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black 1.5pt; padding:0cm 3.55pt 0cm 3.55pt\'>  4	bottom:solid black 1.5pt;border-right:none; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black 1.5pt; padding:0cm 3.55pt 0cm 3.55pt\'>  5	bottom:solid black 1.5pt;border-right:solid black 1.0pt; mso-border-top-alt:solid black .75pt;mso-border-bottom-alt:solid black 1.5pt; mso-border-right-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  6
bottom:none;border-right:solid black 1.5pt;mso-border-left-alt:solid black .75pt; mso-border-right-alt:solid black 1.5pt;padding:0cm 3.55pt 0cm 3.55pt\'>  1	1,00	0,62	0,48	0,39	0,32	0,26	0,22	0,19	0,16	0,08	0,05	0,03	0,01
bottom:none;border-right:solid black 1.5pt;mso-border-left-alt:solid black .75pt; mso-border-right-alt:solid black 1.5pt;padding:0cm 3.55pt 0cm 3.55pt\'>  2	1,00	0,78	0,62	0,47	0,37	0,29	0,22	0,17	0,14	0,05	0,02	0,01	0,00
bottom:none;border-right:solid black 1.5pt;mso-border-left-alt:solid black .75pt; mso-border-right-alt:solid black 1.5pt;padding:0cm 3.55pt 0cm 3.55pt\'>  3	1,00	0,86	0,68	0,52	0,39	0,29	0,21	0,15	0,11	0,03	0,01	0,00	0,00
bottom:none;border-right:solid black 1.5pt;mso-border-left-alt:solid black .75pt; mso-border-right-alt:solid black 1.5pt;padding:0cm 3.55pt 0cm 3.55pt\'>  5	1,00	0,94	0,78	0,59	0,42	0,28	0,19	0,12	0,08	0,01	0,00	0,00	0,00
bottom:none;border-right:solid black 1.5pt;mso-border-left-alt:solid black .75pt; mso-border-right-alt:solid black 1.5pt;padding:0cm 3.55pt 0cm 3.55pt\'>  10	1,00	0,99	0,89	0,68	0,44	0,25	0,13	0,06	0,03	0,00	0,00	0,00	0,00
bottom:solid black 1.0pt;border-right:solid black 1.5pt;mso-border-left-alt: solid black .75pt;mso-border-bottom-alt:solid black .75pt;mso-border-right-alt: solid black 1.5pt;padding:0cm 3.55pt 0cm 3.55pt\'>  15	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  1,00	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  1,00	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  0,94	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  0,73	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  0,45	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  0,23	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  0,10	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  0,04	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  0,01	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  0,00	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  0,00	bottom:solid black 1.0pt; mso-border-bottom-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  0,00	bottom:solid black 1.0pt;border-right:solid black 1.0pt;mso-border-bottom-alt: solid black .75pt;mso-border-right-alt:solid black .75pt;padding:0cm 3.55pt 0cm 3.55pt\'>  0,00