Techniklexikon

Arnold-Zungen

nach W.I. Arnold benannte Gebiete im Parameterraum von periodisch getriebenen, nichtlinearen Oszillatoren mit dissipativer Dynamik Dynamik, in denen die resultierende Oszillatorfrequenz in einem rationalen Verhältnis zur Treiberfrequenz einrastet (Frequenz- oder Mode-Locking). Im Grenzfall starker Dissipation lässt sich die Dynamik im Poincaré-Schnitt häufig auf eindimensionale Kreisabbildungen von der Form q_{n + 1} = f(q_n)mod(2p) reduzieren. Das Mode-Locking drückt sich hier in rationalen Werten der Windungs- oder Rotationszahl  aus.

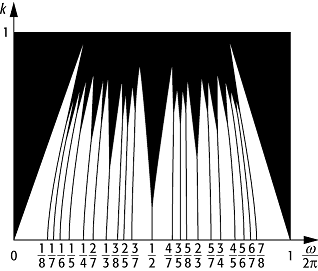
Arnold-Zungen: Arnold-Zungen (schwarz) für die Kreisabbildung f(q) = q + w - k × sinq. Für k = 1 haben w-Intervalle mit irrationalen Rotationszahlen verschwindendes, für k < 1 nicht-verschwindendes Lebesgue-Mass. Für k > 1 findet ein Übergang ins Chaos auf der quasiperiodischen Route statt.