Techniklexikon

Arnold-Diffusion

nach W.I. Arnold benannter chaotischer Diffusionsprozess (chaotische Diffusion), der bei einer generischen Störung eines integrablen Hamilton-Systems einsetzt. Die Diffusion findet entlang des Arnold-Netzes im Phasenraum statt. Dieses wird durch den Schnitt von Resonanzflächen mit einer Energiefläche H₀(I) = E gebildet (Resonanz). Hierbei ist H₀(I) die Hamilton-Funktion des ungestörten, integrablen Systems in den Wirkungsvariablen I. Die Resonanzflächen sind durch die Resonanzbedingungen m × w = 0 definiert, wobei m ein beliebiger Vektor mit ganzzahligen Komponenten und w = ÑH₀(I) der Vektor der Rotationsfrequenzen des ungestörten Systems ist. An Orten im Phasenraum, die die Resonanzbedingungen erfüllen, ist das integrable System besonders empfindlich gegen Störungen. Eine Störung bewirkt dort typischerweise chaotisches Verhalten (Chaos). In Systemen mit drei und mehr Freiheitsgraden kann eine chaotische Trajektorie durch Arnold-Diffusion jedem Ort auf der Energiefläche beliebig nahe kommen.

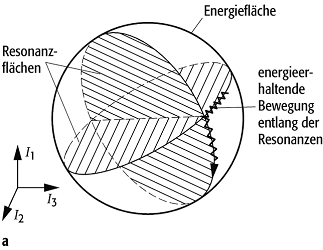
Arnold-Diffusion 1: Zwei sich schneidende Resonanzflächen im Raum der Wirkungsvariablen eines Systems mit drei Freiheitsgraden.
character:line-break\'>
character:line-break\'>

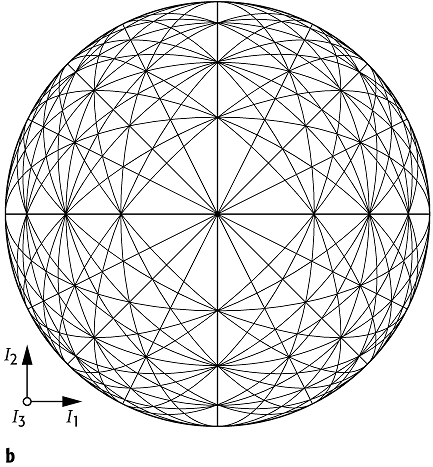
Arnold-Diffusion 2: Teil des Arnold-Netzes für ein freies Teilchen in drei Dimensionen.