Techniklexikon

Bose-Einstein-Kondensation

der von Einstein 1925 theoretisch vorhergesagte Übergang eines Systems ununterscheidbarer Bosonen in denjenigen Zustand (Grundzustand), in dem alle Teilchen die gleiche, niedrigste mögliche Energie haben. Eine solche Kondensation kann nur in Systemen von Teilchen stattfinden, die der Bose-Einstein-Statistik genügen, da in diesem Fall jedes Energieniveau beliebig oft besetzt werden kann. Im Gegensatz dazu können Niveaus von Fermionen aufgrund des Pauli-Prinzips mit maximal einem Teilchen besetzt sein. Beim idealen Bose-Gas hängt die Anzahl N₀ der kondensierten Teilchen unterhalb der Bose-Temperatur T_B gemäss

.

von der Temperatur T  ab, wobei N die gesamte Teilchenzahl bedeutet (Abb.). Das erste makroskopische Quantenphänomen, das qualitativ mit Hilfe der Bose-Einstein-Kondensation interpretiert werden konnte, war die Suprafluidität des Heliumisotops ⁴He (London 1938). Eine quantitative Beschreibung wird dadurch erschwert, dass wegen der recht schwachen Wechselwirkung der ⁴He-Atome untereinander das System kein ideales Gas darstellt (Quantenflüssigkeit). Die experimentelle Realisierung der Bose-Einstein-Kondensation von schwereren Atomen gelang erstmals 1995 C. E. Wieman and E. A. Cornell am Joint Institute of Laboratory Astrophysics (JILA) in Boulder, Colorado. Sie erfordert sehr tiefe Temperaturen (unter 10 ^{- 6} K) und relativ geringe Dichten (etwa 10¹¹ Atome pro mm³), da andernfalls die Atome wegen der im Unterschied zu ⁴He stärkeren Wechselwirkung zu Molekülen oder Clustern kondensieren würden. Erreicht werden diese Bedingungen, indem z.B. Rubidiumatome des Isotops ⁸⁷Rb (wie im JILA-Experiment) bei extrem niedrigem Partialdruck in einer magnetooptischen Falle eingefangen und dann mittels Laser weiter abgekühlt werden.

Die Supraleitfähigkeit vieler Metalle, bei der Leitungselektronen Paare mit Spin null bilden (Cooper-Paare), die ebenfalls der Bose-Einstein-Statistik genügen (BCS-Theorie), ist streng genommen keine Bose-Einstein-Kondensation. Da diese Paare nur unterhalb der Sprungtemperatur existieren, erfolgen Erzeugung und Kondensation der Cooper-Paare gleichzeitig.

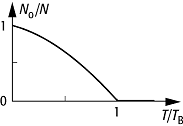
Bose-Einstein-Kondensation: Anzahl der kondensierten Teilchen N₀/N in Abhängigkeit von der Temperatur, T_B: Bose-Temperatur.