Techniklexikon

Fermi-Dirac-Statistik

Kernphysik, Fermi-Statistik, Quantenstatistik für ein aus Fermionen bestehendes und im Gleichgewicht befindliches Vielteilchensystem. Im Unterschied zur klassischen Maxwell-Boltzmann-Statistik sind hier infolge der quantenmechanischen Nichtunterscheidbarkeit der Teilchen Zustände, die sich nur durch den Austausch zweier gleichartiger Teilchen unterscheiden, identisch und dürfen nicht als verschieden gezählt werden. Der wesentliche Unterschied der Fermi-Dirac-Statistik zur Bose-Einstein-Statistik besteht darin, dass die Besetzungszahlen der einzelnen Zustände, die dort unbegrenzt sind, hier nur die Werte 0 und 1 annehmen können. Dies ist eine Folge des Pauli-Prinzips (Fermionen), nach dem sich niemals zwei oder mehr Fermionen im gleichen Quantenzustand befinden können. Ein ideales Fermi-Gas, also ein System aus Fermionen, die nicht miteinander in Wechselwirkung stehen, genügt der Fermi-Dirac-Verteilung . Dabei ist  die mittlere Zahl der Teilchen im Zustand i mit der Energie E_i, k_B die Boltzmann-Konstante und T die absolute Temperatur (Abb. 1). Das chemische Potential m bestimmt sich implizit aus der Gleichung , d.h. die Summe der Teilchenzahlen, summiert über alle Zustände i, ist gleich der Gesamtteilchenzahl N. In der Fermi-Dirac-Statistik kann das chemische Potential auch positive Werte annehmen. g_i ist das statistische Gewicht des Zustandes i, d.h. die Zahl der Quantenzustände mit der Energie E_i. Bei den meisten Anwendungen hat man es mit Fermionen mit dem Spin 1 / 2 zu tun, z.B. mit Elektronen. Es gilt dann g_i = 2 entsprechend den zwei verschiedenen Spinorientierungen je Energiezustand.

Im Falle E_i - m k_BT kann man die 1 im Nenner vernachlässigen, und die Fermi-Verteilung geht über in die Boltzmann-Verteilung. Ist obige Bedingung nicht erfüllt, weicht das Gas in seinen Eigenschaften vom klassischen idealen Gas ab, es tritt Gasentartung ein. Der Verlauf der Besetzungszahl der einzelnen Niveaus in Abhängigkeit von der Energie unter Weglassung des Faktors g_i, also die Funktion

,

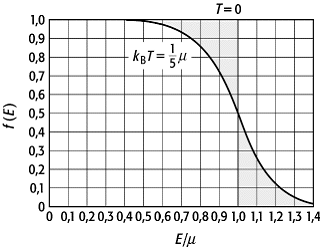
weist folgendes Verhalten auf: Bei tiefen Temperaturen, also bei starker Entartung, besetzen die Fermionen vorwiegend die niederen Energiezustände, während die Zustände höherer Energie praktisch leer sind, wobei der Übergang zwischen besetzten und leeren Energieniveaus in der Nähe des chemischen Potentials je für die entsprechende Temperatur verläuft. Im Grenzfall T = 0 sind alle Zustände unterhalb des chemischen Potentials mit je zwei (für g_i = 2) Fermionen besetzt; die Zustände oberhalb des chemischen Potentials, dessen Grenzwert für T = 0 wegen dieser Eigenschaft auch als Fermi-Energie E_F bezeichnet wird, sind leer. Das bedeutet, dass die mittlere Energie der Fermionen auch am absoluten Nullpunkt nicht verschwindet, sie hat einen endlichen Wert (Abb. 2). Der Fermischen Grenzenergie entspricht bei freien Teilchen ein Grenzimpuls p_F. Alle Fermionen des Systems haben am absoluten Nullpunkt Impulse . Diese Ungleichung beschreibt eine Kugel im Impulsraum, die Fermi-Kugel. Die Zahl der ungleichen Impulszustände innerhalb der Fermi-Kugel ist (4pp_F³ / 3)V / h³, dabei ist V das vorgegebene Volumen des Fermi-Gases.

Von besonderer Bedeutung ist die Anwendung der Fermi-Dirac-Statistik auf das Elektronengas in Metallen, denn dieses befindet sich bereits bei normalen Temperaturen im Zustand starker Entartung. Die Fermi-Dirac-Statistik gestattet praktische Aussagen über die Metalleigenschaften, so z.B. die Herleitung des Richardsonschen Gesetzes der Elektronenemission an Glühkathoden. Auch die mittels der Fermi-Dirac-Statistik berechneten spezifischen Wärmen der Elektronen konnten experimentell bestätigt werden. Die Elektronen liefern bei sehr kleinen Temperaturen den Hauptanteil der spezifischen Wärme des Metalles. Die spezifischen Wärmen verschwinden für T  0 in Übereinstimmung mit dem dritten Hauptsatz der Thermodynamik.

Die Fermi-Dirac-Statistik wurde 1926 von E. Fermi für die Elektronen vorgeschlagen; die theoretische Grundlage gab ihr kurz darauf P.A.M. Dirac, der ihren Zusammenhang mit der Quantentheorie aufdeckte. Die erste Anwendung der Fermi-Dirac-Statistik auf das Elektronengas in Metallen erfolgte durch W. Pauli und A. Sommerfeld.

Fermi-Dirac-Statistik 1: Fermi-Dirac-Verteilung für T = 0 und k_BT = (1 / 5)m. Beide Kurven schneiden sich bei f(E) = 1 / 2.

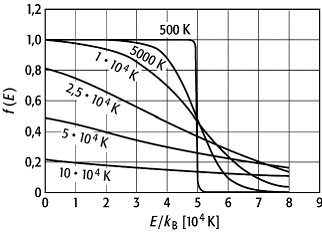
Fermi-Dirac-Statistik 2: Fermi-Dirac-Verteilung für ein Gas in drei Dimensionen, gemessen für verschiedene Temperaturen und E_F / k_B = 50 000 K. Man beachte, dass die Kurven sich nicht bei f(E) = 1 / 2 schneiden.