Techniklexikon

Fraktale

Nichtlineare Dynamik, Chaos, Fraktale

1. Einleitung

Früher waren Fraktale ziemlich selten, heute findet man sie überall. Was ist geschehen? Spätestens seit der zweiten Hälfte des 19. Jahrhunderts war Mathematikern wie Bolzano, Riemann oder Weierstrass klar [1,2], dass es Funktionen gibt, die stetig, aber nirgends differenzierbar sind, also sich von den vorher bekannten analytischen Funktionen fundamental unterscheiden. Heute nennt man solche Funktionen fraktale Funktionen. Die von G. Cantor ebenfalls in dieser Periode eingeführte Cantor-Menge, die das einfachste Beispiel einer fraktalen Menge darstellt ([25]Abb. 1), teilte mit den fraktalen Funktionen lange Zeit das unverdiente Schicksal, als exotisches mathematisches Objekt ohne Bedeutung für natürliche Gegebenheiten zu gelten. Es ist das Verdienst von B.B. Mandelbrot, diesen Zustand grundlegend geändert zu haben. In seinen Büchern [2] zeigte er die Allgegenwärtigkeit fraktaler Strukturen in der Natur auf, sei es durch Betrachtungen der Küstenmorphologie verschiedener Länder, der Struktur von Galaxien-Clustern oder von Preisvariationen und anderen Zeitreihen. Beträchtlichen Aufschwung bekam das Gebiet zudem durch die inzwischen etablierte Erkenntnis, dass das dynamische Verhalten dissipativer Systeme typischerweise durch fraktale Strukturen (Seltsamer Attraktor) gekennzeichnet ist [3], sowie durch die sich in letzter Zeit herauskristallisierende Tatsache, dass viele natürliche Wachstumsprozesse Fraktale generieren [4-6] (fraktales Wachstum).

 

2. Fraktale und ihre Dimension

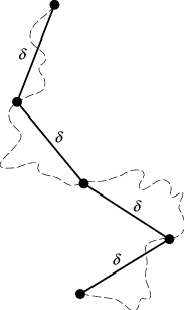
Was sind nun Fraktale? Der Begriff »Fraktal« wurde von Mandelbrot eingeführt, um auszudrücken, dass die zu beschreibenden Objekte meist durch gebrochene, d.h fraktale Dimensionen charakterisiert sind, die grösser als deren topologische Dimension sind. Der Nutzen fraktaler Dimensionen soll an der Messung der Länge von Küstenlinien demonstriert werden. Beim Versuch, die Länge einer Küste zu bestimmen, könnte man auf die Idee kommen, dies in einer Karte durch stückweise Interpolation mit gleich langen Geradenstücken (Massstäben) der Länge d zu tun, in dem man zählt, wie viele solcher Stücke man benötigt ([26]Abb. 2). Sei diese Zahl N(d), so schätzt man die Länge als L(d) = d N(d). Bei dem Verdacht, die Karte wäre möglicherweise zu ungenau gewesen, würde man zu einer detaillierteren Karte mit höherer »Auflösung« greifen und das Experiment mit einem effektiv kürzeren Massstab wiederholen, usw. Bei einer normalen glatten Kurve, wie beispielsweise einem Kreissegment, wird die Verwendung eines immer kleiner werdenden Massstabs ein immer genaueres Resultat für die tatsächliche Länge L^* ergeben, . 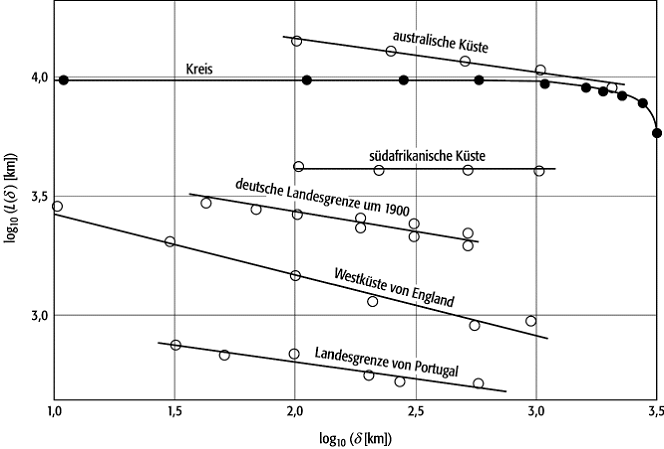Für Küstenlinien findet man, dass die so bestimmte Länge anscheinend divergiert. In [27]Abb. 3 ist dies durch eine Auftragung von log L(d) gegen log (d) dargestellt. Man sieht, dass sich hier für verschiedene Küsten und Ländergrenzen eine lineare Abhängigkeit ergibt (Steigung » -0,25) und somit  bzw. mit D » 1,25 gilt. Das Resultat bedeutet, dass mit feinerem Massstab auch immer feinere Strukturen aufgelöst werden (immer kleinere Buchten und Landzungen), die neue Beiträge zur Länge liefern. Der Exponent D kann als eine fraktale Dimension, also als Verallgemeinerung der üblichen euklidischen Dimension aufgefasst werden. Das macht man sich klar, indem man rekapituliert, wie man Längen, Flächen oder Volumina, also das Mass von »normalen« Objekten bestimmt. Man überdeckt die Objekte z.B. mit dreidimensionalen Kugeln mit Radius d oder Kuben mit Kantenlänge d und bestimmt die benötigte Anzahl N(d). Den Inhalt bekommt man (bis auf eine Konstante) indem man den Grenzwert  bildet. Der ist jedoch nur dann endlich und von null verschieden, wenn d richtig gewählt wird, also d = 1 für (nicht-fraktale) Kurven, d = 2 für flächige Objekte und d = 3 für Volumina. Misst man mit dem »falschen« d, so erhält man als Inhalt null oder unendlich. In dem Küstenbeispiel muss man d = D » 1,25 wählen (wegen ), um ein endliches Mass für die Küstenlänge zu bekommen. Mathematisch präziser formuliert (insbesondere durch Wahl einer auf jeder Skala d optimierten Überdeckung) ist dies das Verfahren zur Bestimmung der Hausdorff-Dimension, der allgemein akzeptierten Definition der fraktalen Dimension eines Objekts. Eine in der Praxis häufig gebrauchte Definition ist die Zellenzahl-Dimension (box counting dimension, Kapazitätsdimension) , wobei N(d) einfach die Anzahl nichtleerer Kästchen auf einem Gitter der Skala d (keine Optimierung) ist. Häufig stimmt diese mit der Hausdorff-Dimension überein (aber z.B. nicht für die Menge der rationalen Zahlen auf dem Einheitsintervall).

Bei der Betrachtung von natürlichen Fraktalen, wie Küstenlinien etc., ist klar, dass ein Skalengesetz, wie , i.A. nicht für beliebige d gilt, sondern in günstigen Fällen über mehrere Dekaden erfüllt ist. D.h. es gibt typischer Weise einen unteren und oberen Abschneideparameter, bei denen andere Gesetzmässigkeiten einsetzen. Im Gegensatz dazu gelten in mathematisch idealisierten Fraktalen die Skalengesetze auch auf infinitesimal kleinen oder unendlich grossen Skalen. Diese idealen Fraktale kann man wiederum danach unterscheiden, ob die Gesetzmässigkeiten deterministischer oder zufälliger Natur sind.

 

2.1 Deterministische Fraktale

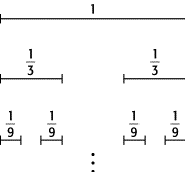
An einigen Beispielen einfacher deterministischer Fraktale sollen deren Gesetzmässigkeiten demonstriert werden. Das einfachste fraktale Objekt ist die triadische Cantor-Menge, wie sie in [28]Abb. 1 dargestellt ist. Bei ihrer Konstruktion wird in einem ersten Schritt aus dem Einheitsintervall das mittlere Drittel entfernt, dann von den verbleibenden Intervallen jeweils wieder das mittlere Drittel, usw. Nach dem n-ten Schritt besteht das sog. Prä-Fraktal aus 2ⁿ Intervallen der Länge (1/3)ⁿ. Im Limes n  ¥ erhält man die Cantor-Menge mit Länge null. Berechnet man die fraktale Dimension nach der Formel

 

auf einem Gitter mit Abständen , so findet man  gefüllte Intervalle und somit

.

Eine wichtige Eigenschaft von Fraktalen, ihre Selbstähnlichkeit, wird durch die Konstruktion der Cantor-Menge offensichtlich: Vergrössert man das Fraktal um einen bestimmten Faktor (hier Faktor 3), so erhält man ein Objekt, das aus disjunkten Teilen besteht (hier 2), die exakte Kopien des ursprünglichen Fraktals sind. Diese Eigenschaft kann man benutzen, um eine fraktale Dimension, die Ähnlichkeitsdimension, zu definieren. Sie ist gegeben durch

und stimmt mit der Hausdorff-Dimension überein.

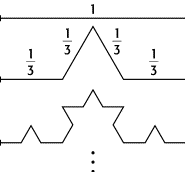
Die fraktale Dimension der klassischen Koch-Kurve, die als deterministisches Modell für Küstenverläufe dienen kann ([29]Abb. 4), ergibt sich aus der Ähnlichkeitsdimension zu .

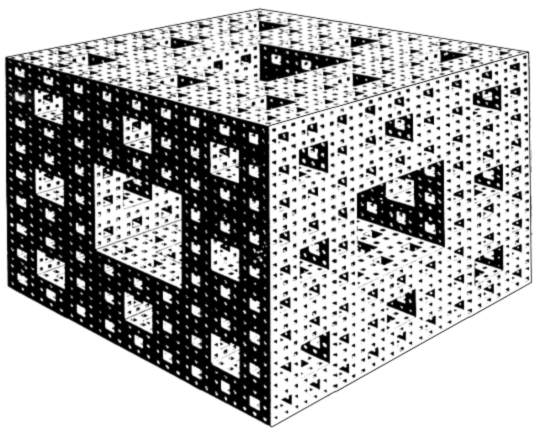
Als letztes Beispiel für deterministische Fraktale sei in [30]Abb. 5 ein fraktales Objekt mit einer Dimension 2 < D < 3 vorgestellt, der Sierpinski-Schwamm (die Projektionen auf die Seitenflächen ergeben jeweils einen sog. Sierpinski-Teppich). Solche Objekte haben eine unendlich grosse Oberfläche und verschwindendes Volumen. Sie können als Modelle für hochporöse Materialien dienen, insbesondere wenn Zufallsaspekte mit berücksichtigt werden.

 

2.2 Zufällige Fraktale

Die strenge Selbstähnlichkeit deterministischer Fraktale ist in natürlich entstandenden fraktalen Strukturen meist nicht gegeben. Letztere sind oft stochastischen Einflüssen durch die Umgebung unterworfen. Deswegen macht es Sinn, Fraktale und entsprechende Modelle zu betrachten, bei denen die Selbstähnlichkeit nur noch statistisch erfüllt ist. Das heisst, dass nach Vergrösserung des Objekts statistisch ähnliche Strukturen vorliegen wie im Ausgangsobjekt. Eine einfache Variation der Cantor-Menge mag dafür als Beispiel dienen. Verschiebt man in jedem Konstruktionsschritt die resultierenden Intervalle nach einer geeigneten Zufallsvorschrift (ohne einen Überlapp der Intervalle zu erzeugen), so wird die strikte Selbstähnlichkeit zerstört, das resultierend Objekt hat aber nach wie vor die gleiche fraktale Dimension. Es gibt eine Reihe anderer durch den Zufall veränderte Varianten dieser Konstruktion, die beispielsweise in der Theorie der Turbulenz eine Rolle spielen.

Das berühmteste Beispiel für zufällige Fraktale sind die Pfade von Brownschen Teilchen, z.B. in einer Dimension (Brownsche Bewegung): Die zeitabhängige Teilchendichte r(x, t), die dem Diffusionsgesetz  (Diffusion) mit Diffusionskonstante  genügt, wird erzeugt durch Ensembles von Trajektorien x(t), die der stochastischen Langevin-Gleichung  genügen, wobei x(t) weisses Gausssches Rauschen mit Mittelwert null ist: .

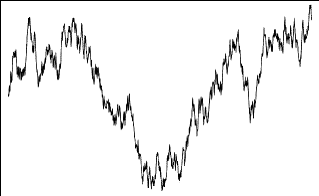
Eine typische Lösung x(t), ein Brownscher Pfad, ist in [31]Abb. 6 dargestellt. Ein neuer Aspekt dieser Lösungsfunktionen ist, dass sie nicht selbstähnlich - auch nicht im statistischen Sinn -, sondern statistisch selbstaffin sind (Selbstaffinität). Dies bedeutet, dass man die Achsen verschieden skalieren muss, um ein statistisch ähnliches Gebilde zu erhalten: Eine Lösung r(x, t) der Diffusionsgleichung erfüllt diese auch nach einer Skalierung . Die Hausdorff-Dimension eines typischen Pfades ergibt sich zu D = 3/2, wie man mit einem Zellenzähl-Argument unter Benutzung der Skalierungseigenschaften nachprüfen kann. Misst man die fraktale Dimension mit der oben geschilderten Massstabsmethode, so erhält man ein anderes Ergebnis, D = 2. Diese Diskrepanz ist eine Besonderheit selbstaffiner Gebilde. Eine Verallgemeinerung der Brownschen Bewegung, die fraktionale Brownsche Bewegung, führt zu fraktalen Dimensionen mit 1 < D < 2. 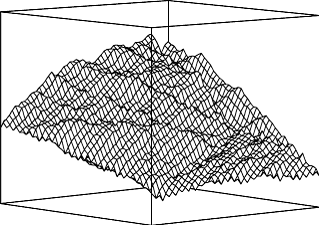Erweiterungen dieser Konzepte auf Funktionen von ²   ergeben fraktale »Gebirge«, die natürlichen Gebirgen sehr ähnlich sehen ([32]Abb. 7). Die klassischen fraktalen Funktionen sind deterministische selbstaffine Fraktale. Zufällige selbstaffine Fraktale spielen beim fraktalen Wachstum eine fundamentale Rolle [4-6].

 

2.3 Multifraktale

In der bisherigen Behandlung fraktaler Mengen wurden keine Annahmen über eventuell vorliegende Verteilungen gemacht, die auf dem Fraktal »leben« könnten. Es wurde ein gegebener Punkt bisher nur danach beurteilt, ob er Teil der Menge ist oder nicht. In physikalischen Problemstellungen sind jedoch typischerweise quantitative Grössen interessant. Man fragt also nicht nur, ob an einem Punkt etwas existiert oder nicht, sondern wieviel. Beispiele für Quantitäten, die auf Fraktalen definiert sein können, sind Teilchendichten, Stromdichten, Konzentrationen chemischer Substanzen in einem Flüssigkeitsgemisch oder allgemein Aufenthaltswahrscheinlichkeiten. 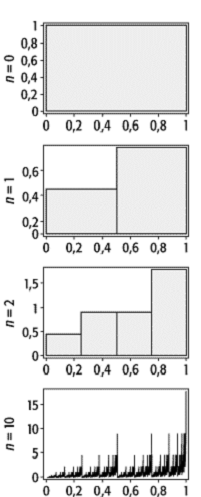Bezieht man solche quantitativen Aspekte mit ein, so untersucht man multifraktale Masse, die auf einem geometrischen Träger definiert sind. Eine einfache iterative Konstruktion soll dies verdeutlichen ([33]Abb. 8). Die Ausgangssituation (n = 0) sei eine normierte Gleichverteilung (von »Masse«) auf dem Einheitsintervall. In einer ersten Iteration (n = 1) wird diese Masse ungleichmässig auf die beiden Hälften des Intervalls verteilt (in [34]Abb. 8: p = 1/3 nach links, 1-p = 2/3 nach rechts), so dass die Gesamtmasse erhalten bleibt. Im nächsten Schritt (n = 2) wird die gleichverteilte Masse der linken Hälfte nach demselben Schema auf dessen Subintervalle (0, 1/4) und (1/4, 1/2) verteilt. Analog verfährt man auf der rechten Seite. Dieser Aufteilungsprozess wird ad infinitum fortgesetzt. Dies ist der binomiale multiplikative Prozess. An der Verteilung, z.B. in Generation n = 10, sieht man, dass die stückweise konstante Massendichte  an vielen Stellen zu divergieren beginnt. 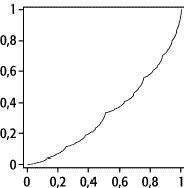Die asymptotische Dichte  ist singulär und mathematisch nicht wohldefiniert, so dass man die integrierten Dichte  betrachtet ([35]Abb. 9). Die Idee der multifraktalen Analyse (Multifraktale) besteht darin, den Träger der Verteilung  in Untermengen gleicher Dichte zu zerlegen (genauer: in Mengen gleichen singulären Verhaltens a im Limes n  ¥), um dann die fraktalen Dimensionen dieser Untermengen zu untersuchen. Die Stärke a der Singularität am Ort x ist definiert durch  für d  0. Die Menge der Punkte mit gleichem (Hölder-) Exponenten a bilden oft eine fraktale Menge, deren Hausdorff-Dimension mit f(a) bezeichnet wird. Die Zerlegung des Trägers der Verteilung nach diesem Schema liefert meist ein Kontinuum von Untermengen mit Skalen-Indizes a, die in einem Intervall [a_min, a_max] liegen, und entsprechend erhält man ein Kontinuum von fraktalen Dimensionen (Multifraktal). f(a) ist daher eine Funktion über [a_min, a_max]. 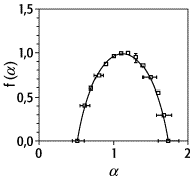Im Falle des binomialen multiplikativen Prozesses kann diese exakt berechnet werden. In [36]Abb. 10 ist sie für p = 0,3 dargestellt und mit Daten aus einem Turbulenz-Experiment [7] verglichen. Das Maximum von f(a) ist die normale fraktale Dimension D₀ des Trägers der multifraktalen Verteilung. In diesem Fall ist D₀ = 1, da der Träger das gesamte Einheitsintervall ist. Eine weitere ausgezeichnete Dimension ist die Informationsdimension D₁, die Hausdorff-Dimension der Menge, auf der fast alle Massenanteile konzentriert sind. Sie kann aus dem f(a)-Graphen als Berührungspunkt mit der Winkelhalbierenden abgelesen werden. Da D₁ < D₀ = 1 gilt, ist die »Masse« auf einer Menge von Lebesgue-Mass null konzentriert. Weitere sogenannte verallgemeinerte Dimensionen D_q, mit -¥ < q < +¥, sind durch t(q) = (q - 1)D_q, die Legendre-Transformierte der konvexen Funktion f(a), definiert (Legendre-Transformation).

 

3. Anwendungen

Die Breite der Anwendungen in fast allen naturwissenschaftlichen Gebieten ist im wesentlichen auf zwei Fraktale erzeugende Mechanismen zurückzuführen. Zum einen entstehen sie auf natürliche Weise als Attraktoren in nichtlinearen dynamischen Systemen, zum anderen als Produkt von Aggregations- oder Wachstumsprozessen. Erstere können aus experimentellen Daten meist erst durch Attraktor-Rekonstruktion gewonnen werden. Ein weiterer Anwendungsbereich sind die spektralen Eigenschaften bestimmter Operatoren, z.B. in der Quantenmechanik, oder Leistungsspektren unendlich langer Sequenzen.

 

3.1 Fraktale in dynamischen Systemen

Es existieren zwei Klassen von dynamischen Systemen, die Fraktale als Attraktoren besitzen. Die eine ist durch deterministische Gleichungen, gewöhnliche Differentialgleichungen oder deterministische iterierte Abbildungen definiert, während die andere Zufallselemente enhält (iterierte Funktionensyteme). Dementsprechend spricht man von deterministischen und von stochastischen dynamischen Systemen. Erstere zeigen typischerweise chaotisches Verhalten auf den Attraktoren (deterministisches Chaos). Das Entstehen fraktaler Attraktoren (Seltsamer Attraktor) kann man leicht an der dissipativen Bäcker-Abbildung nachvollziehen, bei der sich in der kontrahierenden Richtung eine Cantor-Menge ausbildet, oder an topologischen Konstrukten wie dem Smaleschen Hufeisen. Andere bekannte fraktale Attraktoren von Abbildungen oder Differentialgleichungssystemen sind der Hénon-Attraktor (Hénon-Abbildung) oder der Lorenz-Attraktor (Lorenz-System). Ein interessanter Aspekt dieser Systeme ist die Existenz eines Zusammenhangs zwischen fraktaler Dimension des Attraktors und den Liapunow-Exponenten, die den Grad des chaotischen Verhaltens auf dem Attraktor beschreiben (Kaplan-Yorke-Vermutung).

Stochastische dynamische Systeme, die Fraktale generieren (iterierte Funktionensysteme), erlangten grosse Popularität als Basis für mögliche Algorithmen zur Datenkompression (z.B. für natürliche Bilder) [8,9]. Im einfachsten Fall besteht ein solches System aus zwei Funktionen, z.B. g_s(x) = (s + x)/2, s Î {0,1}, und assoziierten Wahrscheinlichkeiten p(s = 0) und p(s = 1) = 1 - p(s = 0). Ein Punkt x₀ wird iteriert, indem die Funktionen g₀ und g₁ in zufälliger, unkorrelierter Reihenfolge mit den zugehörigen Wahrscheinlichkeiten iterativ angewandt werden, . Die (integrierte) Dichte der so erzeugten Punkte konvergiert für n  ¥ mit Wahrscheinlichkeit eins gegen das multifraktale Mass des binomialen multiplikativen Prozesses ([37]Abb. 9: p(s = 0) = 1/3). Mittels Komposition komplexerer Funktionen, z.B. affiner Abbildungen in der Ebene, erhält man »Farne« ([38]Abb. 11) und andere natürlich erscheinende Objekte. Ähnliche stochastische Prozesse treten in vielen anderen Gebieten, z.B. in der statistischen Physik (1 - d Ising-Modell im Zufallsfeld) und bei sequentiellen Lernalgorithmen für neuronale Netze auf.

 

3.2 Fraktales Wachstum

Der Ausbreitungsprozess einer Phase (Aggregatzustand, Cluster, Teilchen, Spezies, etc.) auf Kosten einer anderen findet in den verschiedensten Zusammenhängen, aber oft unter Ausbildung fraktaler Strukturen statt [4-6]. Beispiele sind das Kristallwachstum aus einer unterkühlten Schmelze, die Ausbreitung einer weniger viskosen Flüssigkeit in einer zäheren, elektrolytische Abscheidungen ([39]Abb. 12), Perkolationsprozesse (Perkolation), die Ausbreitung von Bakterienkolonien. Das Wachstum dünner Schichten durch Molekularstrahl-Epitaxie oder durch Sputtern sowie die Ausbreitung von Flammenfronten oder die von Flüssigkeiten in porösen Medien führt häufig zu statistisch selbstaffinen oder fraktalen Grenzflächen. Allen diesen Phänomenen liegt eine Instabilität der wachsenden Grenzfläche zugrunde. Vorhersagen zur Morphologie der Grenzflächen sind oft schwierig, da konkurrierende treibende Kräfte (z.B. Teilchen- oder Wärmediffusion gegen Oberflächenspannung) sowie lokale und nichtlokale Effekte zusammenwirken. Einsichten in die Entstehungsvorgänge werden oft durch einfache mikroskopische Modelle (diffusionsbegrenztes Wachstum, fraktales Wachstum) gewonnen.

 

3.3 Fraktale Spektren

In der Spektraltheorie z.B. von quantenmechanischen Operatoren kennt man neben diskreten Spektren (z.B. Energieniveaus der gebundenen Zustände in Atomen) und kontinuierlichen Spektren (elektronische Bandstruktur in Festkörpern, etc.) eine dritte Klasse, die singulär-stetigen Spektren. Es besteht hier eine Analogie zur Wahrscheinlichkeitstheorie, wo ausser diskreten und kontinuierlichen Wahrscheinlichkeitsverteilungen ebenfalls singulär-stetige Verteilungen ( = multifraktale Masse) existieren. Ein bekanntes Beispiel für ein fraktales Energiespektrum ist der Hofstadter-Schmetterling ([40]Abb. 13), das Spektrum eines quantenmechanischen Modells für Elektronen im Festkörper unter dem Einfluss eines Magnetfeldes [10]. Die Fourier- oder Leistungsspektren komplexer Sequenzen oder Zeitreihen können ebenfalls singulär-stetige Komponenten besitzen. Ein Beispiel einer selbst-ähnlichen Sequenz, für die nicht-triviale f(a)-Kurven für das Fourierspektrum gefunden wurden, ist die zahlentheoretische Thue-Morse-Sequenz, die durch wiederholte parallele Anwendung der Substitutionsregeln 1  1,-1 und -1  -1,1 gewonnen werden kann.

 

3.4 Sonstige Anwendungen

Zum Schluss soll erwähnt werden, dass fraktale Konzepte auch in Bereiche wie Signalanalyse, Bildverarbeitung oder gesellschaftliche Organisationsstrukturen [11] eingeflossen sind.

Literatur:
[1] G.A. Edgar (Hrsg.): Classics on Fractals, Addison Wesley, 1993.
[2] B.B. Mandelbrot: Les Objects Fractals: Forme, Hasard et Dimension, Flammarion 1975.The Fractal Geometry of Nature, W.H. Freeman, 1982.
[3] H.G. Schuster: Deterministic Chaos, VCH-Verlag, 3^rd augm. ed., 1995.
[4] J. Feder: Fractals, Plenum, 1988.
[5] T. Viczek: Fractal Growth Phenomena, World Scientific, 2^nd ed., 1992.
[6] A.-L. Barabási, H.E. Stanley: Fractal Concepts in Surface Growth, Cambridge University Press, 1995.
[7] C. Meneveau, K.R. Sreenivasan: Simple multifractal cascade model for fully developed turbulence, Phys. Rev. Lett. 59, 1424 (1987).
[8] M.F. Barnsley: Fractals Everywhere, Academic Press, 1988.
[9] H.-O. Peitgen et al.: Chaos and Fractals, Springer, 1993.
[10] D.R. Hofstadter: Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields, Phys. Rev. B 14, 2239 (1976).
[11] H.-J. Warnecke: Die fraktale Fabrik: Revolution der Unternehmenskultur. Springer, 1992.

Fraktale 1: Das wiederholte Entfernen des mittleren Drittels des Einheitsintervalls und der jeweils verbleibenden Teilintervalle ergibt die klassische triadische Cantor-Menge. Sie besteht aus unendlich vielen Teilen der Gesamtlänge null und hat die fraktale Dimension D = 0,6309...

Fraktale 2: Längenmessung einer Linie (gestrichelt) mit Massstäben der Länge d. Für normale Kurven konvergiert das Verfahren für d  0, für fraktale Grenzlinien dagegen nicht.

Fraktale 3: Divergenz der Länge L(d) verschiedener Küsten und Landesgrenzen als Funktion der Massstabslänge d (aus [2]).

Fraktale 4: Die iterative Konstruktion der selbstähnlichen Koch-Kurve mit resultierender Dimension D = 1,2618...

Fraktale 5: Der Sierpinski-Schwamm entsteht aus einem Würfel durch wiederholtes Entfernen der zentralen Quader aus den jeweils verbleibenden Würfeln. Sein Dimension ist aufgrund seiner Selbstähnlichkeit (Vergrösserung von drei auf 20 Teile) gegeben durch .

Fraktale 6: Ein Beispiel eines Brownschen Pfades x(t). Die fraktale Dimension dieser statistisch selbstaffinen Kurve ist D = 1,5.

Fraktale 7: Ein fraktales »Gebirge« der Dimension D = 2,3.

Fraktale 8: Die iterative Konstruktion einer multifraktalen Verteilung am Beispiel des binomialen multiplikativen Prozesses.

Fraktale 9: Das multifraktale Mass m(x) zum Prozess aus Abb. 8. Die Funktion m(x) hat fast überall die Ableitung null, sie ist selbstaffin, aber nicht fraktal (Länge = 2).

Fraktale 10: Das multifraktale Spektrum f(a) des binomialen multiplikativen Prozesses für p = 0,3 im Vergleich mit experimentellen Turbulenzdaten [7].

Fraktale 11: Ein iteriertes Funktionensystem, bestehend aus vier affinen Abbildungen in der Ebene, kann »Farne« generieren.

Fraktale 12: Ein durch Kupferabscheidung aus einem schwefelsauren Elektrolyten gewachsenes fraktales Gebilde.

bottom:.0001pt\'>Fraktale 13: Fraktales Energiespektrum (Hofstadter-Schmetterling) für ein Festkörper-Elektron bei Variation eines externen Magnetfelds [10].