Techniklexikon

fraktale Dimension

Nichtlineare Dynamik, Chaos, Fraktale, Grösse zur Charakterisierung fraktaler Objekte und Basis für die Bestimmung ihrer Masse (Fraktale). Sie wird benötigt, da das Messen von Inhalten fraktaler Gebilde in ganzzahligen Dimensionen (Länge, Fläche, Volumen) zu verschwindenden oder divergierenden Werten führt. Die allgemein anerkannte Definition ist die Hausdorff-Dimension. Da diese experimentell und numerisch schwer zu bestimmen ist, benutzt man meist andere Definitionen. Die gebräuchlichste ist die Zellenzähl-Dimension. Sie wird bestimmt, indem in einem euklidischen Raum genügend hoher Dimension ein Gitter mit Gitterkonstante d aufgespannt wird und die Zahl N(d) der durch das Objekt besetzten Gitterzellen festgestellt wird (z.B. Kurve in der Ebene, siehe Abb.). Unter Verfeinerung des Gitters divergiert die Anzahl der benötigten Zellen wie d^-D, wobei D die entsprechende (fraktale oder ganzzahlige) Dimension ist. Als Formel ist sie gegeben durch

.
Sie ist immer grösser oder gleich der Hausdorff-Dimension. Für exakt selbstähnliche Gebilde ist die Ähnlichkeitsdimension definiert als

,

wobei Z die Zahl der disjunkten Teile ist, die sich bei Vergrösserung des Fraktals mit einem Faktor F ergeben, wobei jedes Teil mit dem ursprünglichen Fraktal in Form und Grösse bis auf Verschiebungen und Rotationen identisch sein muss.

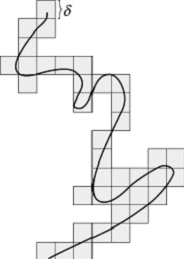
fraktale Dimension: Bestimmung der fraktalen Dimension einer Kurve durch Zählen der besuchten Zellen.