Techniklexikon

Guggenheim-Schema

Thermodynamik und statistische Physik, Guggenheim-Quadrat, Merkschema für die funktionale Abhängigkeit der thermodynamischen Potentiale U (innere Energie), F (freie Energie), H (Enthalpie), G (freie Enthalpie) von ihren Variablen und den Ableitungen nach einer ihrer Variablen, das als Quadrat angeordnet ist (Abb.).(Man kann sich diese Anordnung auch durch den folgenden Spruch im schlechten Deutsch merken: »SUV Hilft Fysikern pei Grossen Taten.«)

Den Kanten dieses Quadrates ist jeweils ein thermodynamisches Potential zugeordnet, den zugehörigen Ecken entsprechend ihre Variablen. Die Ableitung nach einer der an ihren Ecken befindlichen Variablen ist gleich der diagonal entgegengesetzten Grösse, wobei eine sich links befindliche Zielgrösse ein negatives Vorzeichen erhält, eine sich rechts befindliche ein positives Vorzeichen. Bei der Ableitung wird die jeweils andere Variable konstant gehalten.

Beispiel: Die freie Enthalpie G hängt als thermodynamisches Potential vom Druck p und der absoluten Temperatur T ab:
G = G(p, T). Für die Ableitung nach T entnimmt man dem Schema als Ergebnis S mit negativem Vorzeichen, somit ist: .

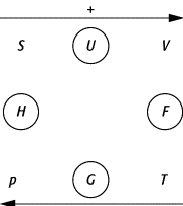
Guggenheim-Schema