Kurvenintegral

Hermann Loring
Mathematische Methoden
und Computereinsatz, Linienintegral, skalarwertiges Integral einer
vektorwertigen Funktion (Vektorfeld) entlang einer Kurve. Sei ![]() eine vektorwertige Funktion und
eine vektorwertige Funktion und ![]() eine Kurve mit Anfangs- und Endpunkten
eine Kurve mit Anfangs- und Endpunkten ![]() und
und ![]() . Dann heisst
das Integral
. Dann heisst
das Integral
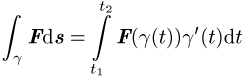
Kurvenintegral. In der
Physik gibt es viele Anwendungen des Kurvenintegrals. Handelt es sich bei F z.B. um ein Kraftfeld, dann stellt das Kurvenintegral
die Arbeit dar, die geleistet wird, wenn man einen Massepunkt vom Punkt ![]() zum Punkt
zum Punkt ![]() entlang der Kurve g verschiebt. Ein
besonders wichtiger Fall liegt vor, wenn es sich um ein divergenzfreies
Vektorfeld handelt, d.h. div F = 0. In diesem Fall
ist der Wert des Kurvenintegrals unabhängig vom Weg bzw. der Kurve g,
also nur von
entlang der Kurve g verschiebt. Ein
besonders wichtiger Fall liegt vor, wenn es sich um ein divergenzfreies
Vektorfeld handelt, d.h. div F = 0. In diesem Fall
ist der Wert des Kurvenintegrals unabhängig vom Weg bzw. der Kurve g,
also nur von ![]() und
und ![]() abhängig. Für geschlossene Kurven, d.h.
abhängig. Für geschlossene Kurven, d.h. ![]() , ergibt sich
daraus die Erhaltung der durch das Kurvebintegral gegebenen physikalischen
Grösse. Es gelten die folgenden Äquivalenzen:
, ergibt sich
daraus die Erhaltung der durch das Kurvebintegral gegebenen physikalischen
Grösse. Es gelten die folgenden Äquivalenzen:
das Kurvenintegral ist wegunabhängig
![]()
F ist konservativ ![]()
F ist konservativ ![]()
F ist Gradientenfeld ![]()
Verwendet man statt ![]() den Körper
den Körper ![]() , so nennt man
das Kurvenintegral auch Kontourintegral. Ein interessantes Ergebnis ergibt
sich, wenn g
die einfach geschlossene Randkurve einer offenen orientierbaren Fläche ist und F stetig-differenzierbar ist. In diesem Fall gilt der
Stokessche Satz:
, so nennt man
das Kurvenintegral auch Kontourintegral. Ein interessantes Ergebnis ergibt
sich, wenn g
die einfach geschlossene Randkurve einer offenen orientierbaren Fläche ist und F stetig-differenzierbar ist. In diesem Fall gilt der
Stokessche Satz:
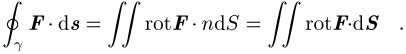
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.