Techniklexikon

Lotka-Volterra-Modell

Laserphysik und -technik, kinetisches Modell der Anzahl der Individuen zweier wechselwirkenden Populationen von Beutetieren der Anzahl N₁ und Raubtieren der Anzahl N₂. Die Beutetiere leben auf der Basis einer Futterreserve A(t), vermehren sich mit der Geschwindigkeit a A(t)N₁ und werden mit der Geschwindigkeit b N₁N₂ von den Raubtieren gefressen. Die Raubtiere leben von den Beutetieren und vermehren sich auf dieser Basis mit der Geschwindigkeit g N₁N₂. Sie sterben mit einer Geschwindigkeit -d N₂. Damit wird die Populationsdynamik von dem Differentialgleichungssystem

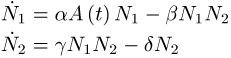
beschrieben mit der Nebenbedingung N_1,2 ³ 0. Wenn sich die Futterreserve in der Zeit nicht ändert, dann ergeben sich typische Sinus- bzw. Sägezahnschwingungen in der Anzahl der Individuen, wobei die Maxima der Anzahl der Raubtiere später als die der Beutetiere auftreten.

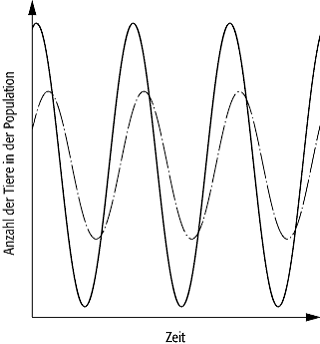
Lotka-Volterra-Modell: Entwicklung der Anzahl der Individuen zweier miteinander wechselwirkenden Populationen mit der Zeit.