Techniklexikon

Monte-Carlo-Methoden

Mathematische Methoden und Computereinsatz, auf Zufallszahlen beruhende Methoden zur Lösung numerischer Probleme. Hierbei wird ausgenutzt, dass eine Teilmenge erzeugter, nicht notwendig gleichverteilter Zufallszahlen bestimmte Eigenschaften erfüllt. Die bekannteste Anwendung dieser Technik ist die Monte-Carlo-Integration. Zu berechnen sei das Integral

über einen Bereich . Seien  und  der Inhalt - für  ist dies die Fläche bzw. für  das Volumen - von  und einer einfacher strukturierten Menge .  könnte z.B. ein mehrdimensionaler Quader sein. Hat man  gleichverteilte Zufallszahlen  erzeugt, von denen  die Relation  erfüllen, so kann das Integral (*) durch

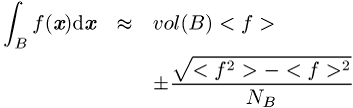
approximiert werden, wobei

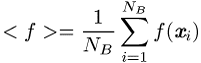
und

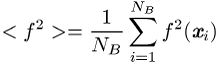
bedeuten und sich , falls nicht anderweitig bekannt, aus

berechnen lässt. In der Praxis versucht man, die Monte-Carlo-Integration mit strukturierten Verfahren zu verbinden, die es erlauben, einen Teil des Problems exakt zu behandeln und nur den nicht so einfach zugänglichen Teil via Monte-Carlo-Integration auszuwerten.