Skalarprodukt

Hans-Peter Ahlsen
Mathematische Methoden
und Computereinsatz, inneres Produkt, positiv definite symmetrische
Bilinearform (bzw. Hermitesche Form) ![]() auf einem Vektorraum
auf einem Vektorraum ![]() über einem Körper
über einem Körper ![]() . Für das
Skalarprodukt findet man in der Literatur die äquivalenten Schreibweisen:
. Für das
Skalarprodukt findet man in der Literatur die äquivalenten Schreibweisen:
![]()
wobei ![]() den zu
den zu ![]() komplex-konjugierten und transponierten Vektor
bezeichnet; im Falle
komplex-konjugierten und transponierten Vektor
bezeichnet; im Falle ![]() ist
ist ![]() . Damit die
Abbildung
. Damit die
Abbildung ![]() Skalarprodukt genannt werden kann, muss sie, im
Falle
Skalarprodukt genannt werden kann, muss sie, im
Falle ![]() , die folgenden
Eigenschaften erfüllen:
, die folgenden
Eigenschaften erfüllen:
positive Definitheit
![]()
Symmetrie
![]()
Linearität in beiden Argumenten
![]()
![]()
und skalare Multiplizität in beiden Argumenten
![]()
![]()
wobei ![]() die zu
die zu ![]() komplex-konjugierte Zahl bezeichnet. Manchmal
findet man auch die Bedingungen
komplex-konjugierte Zahl bezeichnet. Manchmal
findet man auch die Bedingungen ![]() und
und ![]() ; im Falle
; im Falle ![]() gilt schliesslich
gilt schliesslich ![]() .
.
Das Skalarprodukt macht ![]() über
über ![]()
![]() zum euklidischen (unitären) Vektorraum, es
induziert die euklidische Norm und das Konzept der Orthogonalität.
zum euklidischen (unitären) Vektorraum, es
induziert die euklidische Norm und das Konzept der Orthogonalität.
Die in der Physik am häufigsten gebrauchten euklidischen bzw.
unitären Vektorräume sind der Vektorraum ![]() , der
Vektorraum
, der
Vektorraum ![]() der auf dem Intervall
der auf dem Intervall ![]() stetigen Funktionen und speziell in der
Quantenmechanik der Vektorraum
stetigen Funktionen und speziell in der
Quantenmechanik der Vektorraum ![]() der quadratintegrierbaren, komplexwertigen
Funktionen
der quadratintegrierbaren, komplexwertigen
Funktionen ![]() , für die gilt:
, für die gilt:
![]()
der ![]() ist ein Beispiel für einen Hilbert-Raum. Auf dem Vektorraum
ist ein Beispiel für einen Hilbert-Raum. Auf dem Vektorraum ![]() ist das Skalarprodukt definiert als
ist das Skalarprodukt definiert als
![]()
In diesem Fall kann mit Hilfe des Skalarprodukts der Winkel ![]() zwischen von Null verschiedenen Vektoren
zwischen von Null verschiedenen Vektoren ![]() und
und ![]() berechnet werden:
berechnet werden:
![]()
wobei ![]() die euklidische Norm bezeichnet. Auf dem
Funktionenvektorraum
die euklidische Norm bezeichnet. Auf dem
Funktionenvektorraum ![]() mit z.B. komplex-wertigen Funktionen
mit z.B. komplex-wertigen Funktionen ![]() und
und ![]() ist das Skalarprodukt definiert als
ist das Skalarprodukt definiert als
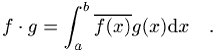
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.