Techniklexikon

Ameise im Labyrinth

in der statistischen Physik die auf de Gennes zurückgehende Bezeichnung für das Problem der Zufallswege bzw. der Diffusion auf Clustern. Der Zufallsweg auf einem Cluster wird durch eine Ameise symbolisiert, die an einem beliebigen Clusterpunkt startet und für die jeder Schritt auf diesem Cluster unabhängig von den vorherigen Schritten ist. Blinde Ameisen gehen mit derselben Wahrscheinlichkeit in jede mögliche Gitterrichtung, können jedoch nur dann voranschreiten, wenn diese Gitterrichtung auch Teil des Clusters ist. Kurzsichtige Ameisen hingegen erkennen, welche Richtungen innerhalb des Clusters möglich sind, und wählen nur eine von diesen.

Beschrieben wird der Zufallsweg durch die Wahrscheinlichkeit , dass die Ameise, die am Punkt x₀ startet, sich nach t Schritten am Punkt x befindet.  ist Lösung einer Master-Gleichung der Form

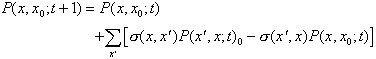
wobei  die Wahrscheinlichkeit ist, in einem Schritt vom Punkt  zum Punkt x zu gelangen. Diese Master-Gleichung entspricht auf dem Cluster einer diskretisierten Diffusionsgleichung (Diffusion).

Von besonderer Bedeutung ist der mittlere zurückgelegte Abstand R(t) auf dem Cluster nach t Schritten:

.

Bei einem unendlichen Cluster erwartet man im Grenzfall  ein Diffusionsgesetz der Form . Ist J ¹ 1, so spricht man von einer anomalen Diffusion, J bezeichnet man als den anomalen Diffusionsexponenten.