Techniklexikon

Master-Gleichung

Thermodynamik und statistische Physik, von Prigogine und Résibois 1961 erstmals abgeleitete partielle Differentialgleichung der Statistischen Physik des Ungleichgewichtszustandes zur Beschreibung stochastischer Prozesse, die in diesem Zusammenhang als eine bestimmte Unterklasse von Markow-Prozessen dargestellt werden. Sie beschreibt das Langzeitverhalten der Übergangswahrscheinlichkeit , also der Wahrscheinlichkeit, dass die betrachtete Zufallsvariable Y(t) zur Zeit t₂ den Wert y₂ annimmt unter der Voraussetzung, dass sie zur Zeit t₁ den Wert y₁ durchlaufen hat, und hat die Form

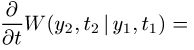
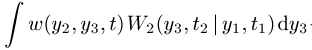
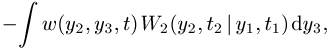
wobei  die Übergangswahrscheinlichkeit zwischen den Werten y₂ und y₃ angibt. Ist die betrachtete Zufallsvariable eine diskrete Zahl n, so nimmt diese Master-Gleichung ihre bekanntere Form mit der Wahrscheinlichkeit p_n(t) für das Auftreten des Wertes n zur Zeit t und der Ersetzung  an:

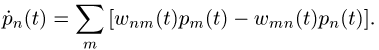
Die Wahrscheinlichkeit, zur Zeit t den Wert n vorzufinden, setzt sich also aus einem Gewinnterm (Übergänge n  m) und einem Verlustterm (Übergänge m  n) zusammen. In dieser Form kann die Master-Gleichung als eine Bewegungsgleichung für die Besetzungswahrscheinlichkeiten p_n von Systemzuständen n bei Nichtgleichgewichtsprozessen verstanden werden.