Techniklexikon

Heisenberg-Spinkette

quantenmechanisches eindimensionales Gittermodell, bei dem den Punkten der Gitterkette Spin-Matrizen zugeordnet werden (Heisenberg-Modell). Seien beispielsweise , ,  die Pauli-Spin-Matrizen am Gitterpunkt i, so ist der Hamilton-Operator der Heisenberg-Spinkette durch

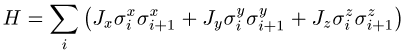
gegeben. J_x, J_y und J_z sind Kopplungskonstanten. Sind alle drei Kopplungskonstanten verschieden, so spricht man auch von der XYZ-Heisenberg-Spinkette (oder einfacher vom XYZ-Modell). Sind zwei Kopplungskonstanten gleich (beispielsweise J_x = J_y), so bezeichnet man das Modell als XXZ-Heisenberg-Spinkette (bzw. XXZ-Modell), sind alle drei Kopplungen identisch, so spricht man vom XXX-Modell.

Über den Transfermatrix-Formalismus ist das XYZ-Modell äquivalent zum Acht-Vertex-Modell und das XXZ-Modell äquivalent zum Sechs-Vertex-Modell.