Techniklexikon

Hyperbel

ebene geometrische Figur, die zu den Kegelschnitten gehört. Sie ist der Ort aller Punkte, für die die Differenz der Abstände von zwei festen Punkten F und F\' konstant ist. Sie besteht stets aus zwei Ästen. Die Elemente der Hyperbel sind die reelle Achse ; die Scheitel A, B; der Mittelpunkt O; die Brennpunkte F, F\', die auf der reellen Achse auf beiden Seiten des Mittelpunktes im Abstand c (> a) liegen; die imaginäre Achse ; der Halbparameter p = b² / a, d.h. die halbe Länge der Sehne, die durch einen Brennpunkt zur reellen Achse gelegt wird; und die numerische Exzentrizität e = (c / a) > 1 (Abb. 1).

Für die Hyperbel gilt die Normalform

(Mittelpunktsgleichung). Asymptoten der Hyperbel sind Geraden, denen sich die Hyperbelzweige im Unendlichen nähern, mit den Gleichungen y = ±(b / a) · x. Für den Winkel der beiden Asymptoten gilt tan J = b / a. Die Asymptotenform der Hyperbel ist xy = (a² + b²) / 4 = e² / 4 = const. Die Leitlinien sind zur reellen Achse senkrechte Geraden, die sie in der Entfernung d = a / e vom Mittelpunkt schneiden; für beliebige Punkte M auf der Hyperbel gilt r₁ / d₁ = r₂ / d₂ = e.

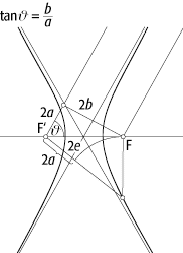
Hyperbel 1: Elemente der Hyperbel.

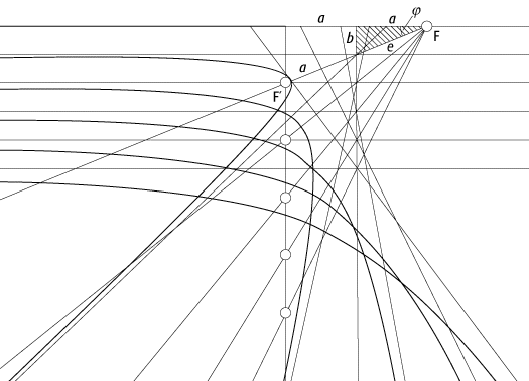
Hyperbel 2: Eine Schar von Hyperbelbahnen, die sich bei der Streuung an einem Streuzentrum in F ergeben. Die Gesamtenergie (d.h. die grosse Halbachse a) ist jeweils gleich, die Stossparameter (kleine Halbachsen b) sind verschieden. Daher unterscheiden sich auch die numerischen Exzentritäten e und die Streuwinkel j.