Techniklexikon

Integralrechnung

Teilgebiet der mathematischen Analysis, das sich mit der Integration von Funktionen beschäftigt und zusammen mit der Differentialrechnung die Infinitesimalrechnung bildet. Der Integralbegriff, der noch relativ nahe mit der Wurzel der Integralrechnung, dem Problem der Inhaltsbestimmung geometrischer Körper, verbunden ist, ist das Riemann-Integral der R-integrierbaren Funktionen, die sich aus einfachen Treppenfunktionen gewinnen lassen; eine vollständige Charakterisierung der R-integrierbaren Funktionen als diejenigen Funktionen, deren Unstetigkeitsstellen eine Nullmenge ist, liefert das Lebesgue-Integral. Die Berechnung des Riemann-Integrals liefert der Hauptsatz der Integralberechnung über die Differenz der Funktionswerte einer Stammfunktion an den Grenzen des Integrals: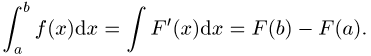

Ein wesentlicher Teil der Integralberechnung besteht demnach in der Suche nach Stammfunktionen. In diesem Zusammenhang hat sich der Begriff des unbestimmten Integrals eingebürgert, mit dessen Hilfe sich die meisten Integrationsregeln formulieren lassen. Für die mathematische und physikalische Praxis stehen umfangreiche Integralsammlungen zur Verfügung (siehe Vorsatzseiten).

Der Begriff des Riemann-Integrals lässt sich auch auf mehrere Variablen ausdehnen. Sind die zu integrierenden Funktionen auf Kurven und Flächen im  definiert (Vektorfelder), erhält man die in der Physik sehr wichtigen Begriffe der Kurven- und Oberflächenintegrale, die mit den Riemann-Integralen über Integralsätze (Gaussscher Satz, Stokesscher Satz) verknüpft sind.