Techniklexikon

Korrelationsdimension

von P. Grassberger und I. Procaccia 1983 eingeführter Dimensionsbegriff zur Charakterisierung fraktaler Mengen (z.B. chaotischer Attraktoren), der insbesondere bei der Analyse experimenteller Zeitreihen eingesetzt wird. Die Definition der Korrelationsdimension beruht auf der Korrelationssumme , die angibt, mit welcher Wahrscheinlichkeit zwei Punkte  und  der Menge einen Abstand kleiner  besitzen. Mit Hilfe der Heaviside-Funktion H ( falls  und  falls ) lässt sich die Korrelationssumme definieren als

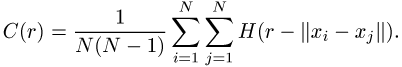
Die Korrelationsdimension

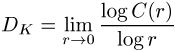
beschreibt das Skalierungsverhalten von  für kleine Abstände r und wird in der Regel durch doppellogarithmische Auftragung  gegen  bestimmt. Die Korrelationsdimension ist invariant bezüglich fast aller stetig differenzierbaren Koordinatensystemwechsel und stimmt approximativ mit der Rényi-Dimension  überein.