Techniklexikon

Korrelationsfunktion

Laboratoriumsmethoden und -geräte, das gemischte Moment

 

zweier zufälliger Prozesse x(t) und y(t) unter Berücksichtigung einer zeitlichen Verzögerung t des einen Prozesses gegenüber dem anderen, wobei Ex(t) und Ey(t) die Erwartungs- bzw. Mittelwerte der jeweiligen Prozesse sind. Für stationäre zufällige Prozesse, bei denen die Wahl eines zeitlichen Bezugspunktes auf seine Eigenschaften keinen Einfluss hat, hängt die Korrelationsfunktion nur von der Verzögerungszeit t ab. Die praktische Bedeutung der Korrelationsfunktion ergibt sich aus ihrer Rolle als Abhängigkeitsmass. So ist die Korrelationsfunktion Null, wenn die Zufallsprozesse x(t) und y(t - t) voneinander statistisch unabhängig sind.

In der statistischen Physik dient die Korrelationsfunktion zur Charakterisierung des Zusammenhanges zweier gleichzeitig verlaufender Schwankungsvorgänge, die durch die Zeitfunktionen x(t) und y(t) beschrieben werden können. Die Korrelationsfunktion berechnet sich für einen im Zeitnullpunkt startenden Prozess nach der Formel

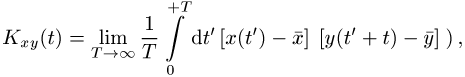
wobei  und  die Mittelwerte der jeweiligen Prozesse sind. Bei normierten und zeitsymmetrischen Zufallsprozessen benutzt man als Korrelationsfunktion häufig auch den Ausdruck

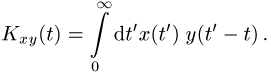
Bei der Autokorrelationsfunktion wird die Schwankungsgrösse mit sich selbst, gleichfalls zeitverschoben, untersucht, indem man die Funktion y(t) in voriger Formel durch x(t) ersetzt.

Bei zeitlichen Prozessen wird oft das asymptotische Verhalten für grosse Zeiten t untersucht. Man erwartet, dass die Korrelationsfunktion mehr oder weniger rasch abnimmt. Da viele physikalische Prozesse ein exponentielles Abklingverhalten mit  zeigen, ist die Korrelationszeit t ein Mass für die Stärke der Korrelation. Es sind aber auch Korrelationsfunktion mit algebraisch abfallendem Verlauf bekannt, die gegenüber dem exponentiellen Abfall bei grösseren Zeiten stets ein langsameres Abklingverhalten aufweisen.

Besondere Bedeutung besitzt die Korrelationsfunktion vor allem dadurch, dass sie einen  Zusammenhang mit der Temperatur T des Systems herstellt. Dieser wird durch das Schwankungs-Dissipations-Theorem zum Ausdruck gebracht. Für die Fourier-Transformierte  der Korrelationsfunktion gilt demnach

wobei k die Boltzmann-Konstante und c(t) eine prozessspezifische Dissipationsfunktion (Suszeptibilität) ist. Ausserdem besteht zwischen der Korrelationsfunktion und der Spektraldichte durch das Wiener-Khinchine-Theorem ein eindeutiger Zusammenhang.

Zufallsschwankungen treten jedoch nicht nur in zeitlicher Folge auf, für ungeordnete Systeme ist die räumliche Position r der Atome oder Moleküle ebenfalls eine Zufallsgrösse. Eine einfache Beschreibungsgrösse für deren gegenseitige Wechselwirkung erfolgt durch die Korrelationsfunktion g(r), die auch radiale Verteilungsfunktion genannt wird.

Im Falle vieler Teilchen N steht sie mit der Paar-Verteilungsfunktion  (r₁, r₂: Positionsvektoren der Moleküle 1 und 2, V: Volumen, T: Temperatur) in enger Beziehung und kann auch auf verschiedenatomige Systeme angewendet werden. Da die Paar-Verteilungsfunktion für Flüssigkeiten und Gase nur vom gegenseitigen Abstand abhängt, wird sie durch  definiert, wobei r die Teilchendichte ist. Im Falle idealer Gase, d.h. Teilchen ohne Wechselwirkung und damit mit einem Wechselwirkungspotential , gilt , d.h. hierfür ist . Hingegen erhält man bei periodischen Anordnungen in Kristallen einen periodischen Verlauf der Korrelationsfunktion. Bei vielen ungeordneten Systeme erfolgt die Konvergenz mit wachsender Entfernung r in exponentieller Weise. Hierbei ist der Korrelationsradius ein Mass für die Stärke des Abfalls. Im Falle von Edelgasen erfolgt sie besonders rasch, weshalb Edelgase den idealen Gasen im thermodynamischen Verhalten ähneln. Bei anderen Strukturen, so etwa bei Gläsern, kann die Korrelation aufgrund der Netzwerkstruktur weitreichend sein; sie muss auch nicht mehr exponentiell abnehmen.

Die Stärke der Korrelation und damit die Paarverteilungsfunktion hat Einfluss auf das thermodynamische Verhalten des Systems. Aus ihrer Kenntnis lässt sich die thermische Zustandsgleichung ableiten.