Techniklexikon

Lagrange-Gleichungen

fundamentale Form der Bewegungsgleichungen der Mechanik. Unterliegt ein System mit N Freiheitsgraden n holonomen Zwangsbedingungen, so lauten die Lagrange-Gleichungen für die N - n = i verallgemeinerten Koordinaten q_i

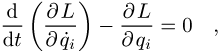
in denen die Lagrange-Funktion L sich als Differenz der kinetischen Energie T und der potentiellen Energie V ergibt.

Aufgrund ihrer Einfachheit und ihrer idealen Angepasstheit an holonome Zwangsbedingungen - die Zwangskräfte erscheinen nicht explizit, die Anzahl der Gleichungen entspricht derjenigen der realen Freiheitsgrade des Systems - eignen sich die Lagrange-Gleichungen in der Regel von allen Formalismen am besten zur Aufstellung der Bewegungsgleichungen. (Analytische Mechanik)