Techniklexikon

Laurent-Reihe

die von P.A. Laurent im Jahre 1843 eingeführte und nach ihm benannte, aber bereits 1841 von Weierstrass entdeckte Reihe der Form

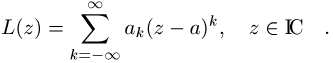
Die Partialsumme  heisst Hauptteil, die Summe  Nebenteil der Laurent-Reihe. Ist f(z) eine auf dem offenen Kreisring  holomorphe Funktion (analytische Funktion), dann existiert die Darstellung

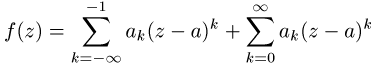
mit den Koeffizienten

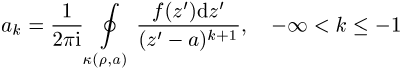
für den Hauptteil; diese Koeffizienten lassen sich meist mit Hilfe des Residuensatzes berechnen. Der Nebenteil der Laurent-Reihe entspricht gerade der Taylor-Reihe von f. Laurent-Reihen sind damit eine Verallgemeinerung der Taylor-Reihen. Beispiel: Die in  holomorphe Funktion

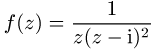
besitzt in  die Laurent-Reihe

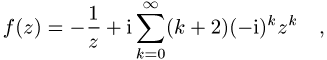
in  dagegen die Laurent-Reihe

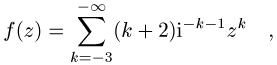
sie besteht dort also nur aus dem Hauptteil.