Techniklexikon

numerische Differentiation

Mathematische Methoden und Computereinsatz, die numerische Berechnung von Ableitungen. Im einfachsten Fall ist die erste Ableitung  zu ermitteln, die für eine vorgegebene, hinreichend kleine Zahl  wegen der Definition der Ableitung als  intuitiv auf die (asymmetrische) Näherung

führt, d.h. der Differentialquotient wird durch den Differenzenquotienten ersetzt. Wegen des Rundungs- und Abbruchfehlers (Diskretisierungsfehler) ist diese Operation kaum empfehlenswert. Die Taylor-Reihenentwicklung

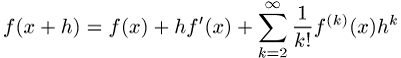
zeigt nämlich, dass der Abbruchfehler  linear in  ist. Hingegen ist der Abbruchfehler bei der (symmetrischen) Approximation (Verwendung zentraler Differenzen) }

nur von der Grössenordnung . Die numerische Differentiation und ihre Anwendungen auf höhere oder partielle Ableitungen lässt sich allgemein mit Hilfe des Operators  mit ,  und

beschreiben; alternativ ergibt sich bei Verwendung zentraler Differenzen  und  noch die Beziehung

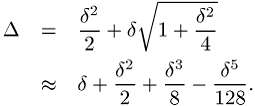
Beispiel: Die Taylor-Reihenentwicklung von  ergibt

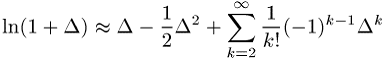
und bei Abbruch nach dem ersten Term schliesslich

bzw. in zentralen Differenzen

Der Abbruch nach dem zweiten Term der Taylorreihe liefert hingegen  mit

und somit schliesslich

allerdings ist diese Näherung der symmetrischen Approximation unterlegen; bei beiden wächst der Approximationsfehler zwar mit , (*) hat jedoch den kleineren Vorfaktor. Die zweite Ableitung folgt mit  zu

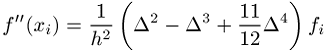
bzw. bei Abbruch nach

Wegen des Rundungsfehlers und möglicher Auslöschung von Ziffern durch Differenzbildung ist die Wahl von  sehr kritisch. Bezeichnet  die relative Genauigkeit, mit der  berechnet wird, so sollte bei der symmetrischen Approximation von  das Inkrement  als

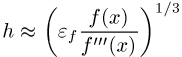
gewählt werden.

Eine numerische effiziente Berechnung der Ableitung kann man in analoger Weise zum Romberg-Verfahren durch Extrapolation gewinnen.