Techniklexikon

reziprokes Gitter

Festkörperphysik, wichtiges mathematisches Hilfsmittel zur Beschreibung und Diskussion von Beugungsphänomenen an Kristallen. Das reziproke Gitter ist ein Translationsgitter, welches durch die Basisvektoren  (, den reziproken Gittervektoren, aufgespannt wird. Diese Basisvektoren stehen mit den Basisvektoren  des realen Kristallgitters in folgender Beziehung:

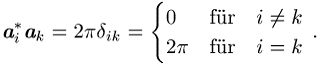
Das bedeutet :

 steht senkrecht auf a₂ und a₃ (also senkrecht auf der Netzebenenschar 100),

 steht senkrecht auf a₃ und a₁ (also senkrecht auf der Netzebenenschar 010),

 steht senkrecht auf a₁ und a₂ (also senkrecht auf der Netzebenenschar 001).

Die Längen der reziproken Gittervektoren sind reziprok zu den Abständen der Netzebenen :

Das reziproke Gitter definiert den reziproken Raum und ist jedem realen Gitter eindeutig zugeordnet; seine Gitterpunkte werden durch die ganzen Zahlen  bezeichnet.

Die Basisvektoren des reziproken Gitters lassen sich wie folgt berechnen:

und zyklisch.

Aus der eindeutigen Zuordnung von realem Gitter und reziprokem Gitter folgt, dass jede Deckoperation des Gitters auch zu einem deckungsgleichen realen Gitter führen muss. Das reziproke Gitter gehört also der gleichen Punktgruppe wie das reale Gitter an.

Mit Hilfe des reziproken Gitters lassen sich in der Ewald-Konstruktion in einfacher geometrischer Weise die verschiedensten Reflexionsbedingungen überblicken und diskutieren