Techniklexikon

Runge-Kutta-Verfahren

Mathematische Methoden und Computereinsatz, Einschrittverfahren  zur Integration gewöhnlicher Differentialgleichungen , die den Vorzug haben, Terme höherer Ordnung einer Taylor-Reihenentwicklung von verfahren.gif" alt="Runge-Kutta-Verfahren"> zu verwenden, ohne dabei jedoch die höheren Ableitungen ausrechnen zu müssen. Die Grundidee besteht darin, die Taylor-Reihenentwicklung  n-ter Ordnung von verfahren.gif" alt="Runge-Kutta-Verfahren"> durch Ausdrücke der Form verfahren.gif" alt="Runge-Kutta-Verfahren"> mit  und für

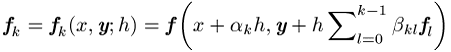
zu ersetzen, wobei eine möglichst hohe Approximationsgüte erzielt werden soll; es kann ein Verfahren n-ter Ordnung gewonnen werden. Die bekannteste Variante ist wohl das Runge-Kutta-Verfahren vierter Ordnung , für das gilt:  und . Verfahren zweiter Ordnung (Verfahren von Heun, modifiziertes Euler-Verfahren = Mittelpunkt-Regel) lassen sich mit verfahren.gif" alt="Runge-Kutta-Verfahren"> und  oder  und  konstruieren. Das Euler-Verfahren (Euler-Cauchy-Verfahren) selbst ist ein Verfahren erster Ordnung  mit  und .

Schliesslich können Runge-Kutta-Methoden mit einer adaptiven Schrittweitensteuerung kombiniert werden.