Suszeptibilitätsellipsoid

Petra Nordinghaus-Martin
Festkörperphysik,
Ellipsoid zur graphischen Bestimmung der magnetischen Suszeptibilität c
in anisotropen Materialien (Anisotropie, magnetische Anisotropie) sowie analog
der elektrischen Suszeptibilität. Die Suszeptibilität ist kein Skalar, sondern
ein Tensor, so dass der Magnetisierungsvektor M = m0cH (m0: absolute
Permeabilität) nichtlinear vom magnetischen Feldvektor H
abhängt, d.h. die Magnetisierbarkeit durch die Richtungswinkel a,
b,
g
von H bezüglich der Kristallachsen bestimmt ist.
Man definiert deshalb auch die skalare Suszeptibilität c(a, b,
g)
mit Hilfe der Komponente ![]() (H = |H|) von M in Richtung von H durch MH
= m0 c(a, b,
g)
H. Wählt man das Hauptachsensystem als
Koordinatensystem (Hauptachsentransformation), erhält man die Beziehung
(H = |H|) von M in Richtung von H durch MH
= m0 c(a, b,
g)
H. Wählt man das Hauptachsensystem als
Koordinatensystem (Hauptachsentransformation), erhält man die Beziehung
![]()
die ein Ellipsoid mit den Hauptachsen ![]() ,
, ![]() und
und ![]() beschreibt. c(a, b,
g)
ergibt sich aus dem Radius
beschreibt. c(a, b,
g)
ergibt sich aus dem Radius ![]() , der in
Richtung des Magnetfeldes H liegt (siehe Abb.).
Der Magnetisierungsvektor M weist in Richtung des
Nomalenvektors des Ellipsoids und hat den Betrag
, der in
Richtung des Magnetfeldes H liegt (siehe Abb.).
Der Magnetisierungsvektor M weist in Richtung des
Nomalenvektors des Ellipsoids und hat den Betrag
![]()
wobei h den Abstand der Tangentialebene zum Mittelpunkt bezeichnet.
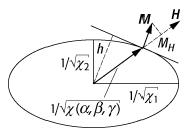
Suszeptibilitätsellipsoid: Schnitt durch ein Suszeptibilitätsellipsoid in der H-M-Ebene für ein magnetisch anisotropes System.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.