Techniklexikon

Young-Diagramm

Mathematische Methoden und Computereinsatz, Young-Tableau, in der Gruppentheorie sehr praktisches Werkzeug zum Studium der irreduziblen Darstellungen der Gruppe  und ihrer Untergruppen, insbesondere SU(N). Man erhält jede Darstellung von SU(N) durch Tensorprodukte seiner fundamentalen Darstellung. Die Elemente im Darstellungsraum der Tensordarstellungen sind also Tensoren, die bestimmte Symmetrieeigenschaften unter Permutationen besitzen. Diese Eigenschaften spiegeln sich in den Young-Diagrammen wider; sie erlauben eine explizite Ableitung der Form der Vektoren im Darstellungsraum und lassen sich zudem dazu benutzen, das Produkt zweier SU(N)-Darstellungen in irreduzible Darstellungen zu zerlegen.

Ein Young-Diagramm besteht allgemein aus einer bestimmten Anzahl Kästchen, die in untereinander liegenden Reihen angeordnet sind, wobei die Zahl der Kästchen in einer Reihe nicht kleiner als die Kästchenzahl in der Reihe darunter sein darf. n horizontale Kästchen haben die Bedeutung eines Tensors vom Rang n mit symmetrisierten Indizes; die Anzahl der unabhängigen Komponenten in einer Reihe ist für SU(N) durch

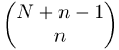
gegeben. Zwei übereinanderstehende Kästchen bedeuten die antisymmetrische Kombination der beiden Indizes eines Tensors vom Rang 2; allgemeiner bedeuten m übereinander stehende Kästchen m antisymmetrisierte Indizes mit der Dimension

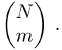
N vertikale Kästchen symbolisieren für SU(N) also einen Tensor mit nur einem unabhängigen Element, der mit 1 bezeichnet wird. Ein beliebiger gemischter Tensor besteht aus mehreren Kästchen, die sowohl über- als auch untereinander angeordnet sein können. Wenn f_i die Anzahl der Kästchen in der i-ten Reihe ist (), kann einem beliebigen Young-Diagramm die Ziffernfolge (f₁, f₂, ¼, f_k) zugewiesen werden. Jede irreduzible Darstellung D(l₁, ¼,l_N-1) von SU(N) kann nun mit dem Young-Diagramm (f_1,N, f_2,N, ¼, f_N-1,N) assoziiert werden, wobei

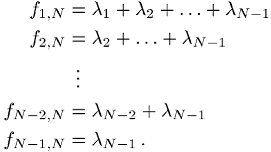
Durch Permutation der Kästchen des so konstruierten Young-Diagramms kann man dann alle Zustände einer SU(N)-Darstellung gewinnen. Die Zerlegung eines (i.a. reduziblen) Produktes zweier Darstellungen D und  in irreduzible Darstellungen erhält man, indem man die Kästchen von  so an das Young-Diagramm von D anfügt, dass wieder ein Young-Diagramm entsteht, und einige weitere Regeln eingehalten werden (siehe Abb. 2 als Beispiel für SU(3)).

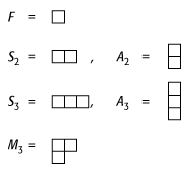
Young-Diagramm 1: Aus der fundamentalen Darstellung F lassen sich symmetrische (S₂, S₃) und antisymmetrische (A₂, A₃) sowie gemischte (M₃) Darstellungen konstruieren.

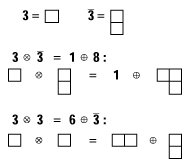
Young-Diagramm 2: Die irreduziblen Darstellungen der SU(3). Das Produkt aus Quark (3) und Antiquark () ergibt ein Oktett und ein Singlett, zwei Quarks ergeben ein Antitriplett und ein Sextett.