Techniklexikon

Einstein-Lobatschewski-Geometrie des Geschwindigkeitsraumes

Relativitätstheorie und Gravitation, dem Additionstheorem der Geschwindigkeiten entsprechende Metrik des Raumes der Geschwindigkeitsvektoren im dreidimensionalen euklidischen Raum (Spezielle Relativitätstheorie). Der Betrag der Relativitätsgeschwindigkeit zweier Körper, die sich gegen ein Bezugssystem S mit  v  und  v  + d v  bewegen, lautet

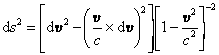
Dieser Ausdruck ist unabhängig vom speziellen Bezugssystem S. Die Länge eines endlichen Relativgeschwindigkeitsvektors ist . Hierbei ist s die nach (1) berechnete Länge der Verbindungegeraden von  v ₁ nach  v ₂ und c die Vakuumlichtgeschwindigkeit. Das Additionstheorem paralleler Relativgeschwindigkeiten gleicht damit dem Additionsgesetz des hyperbolischen Tangens (Lorentz-Gruppe). Mit der Metrik (1) ist der Geschwindigkeitsraum ein dreidimensionaler Raum konstanter negativer Krümmung. Die Transformation
  
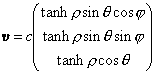
liefert die Standardform der Metrik eines solchen Raumes:

.