Einstein-Maxwellsche Gleichungen

Martina Wagner
(G)Elektrodynamik und Elektrotechnik, Gleichungssystem, das die Ankopplung des elektromagnetischen Feldes an das Gravitationsfeld im Rahmen der Allgemeinen Relativitätstheorie mit Hilfe des Einsteinschen Äquivalenzprinzips beschreibt.
Dabei wird der Energie-Impuls-Tensor T mn
des elektromagnetischen Feldes als Quelle des Gravitationsfeldes gmn
in die Einstein-Gleichungen eingesetzt (![]() :
Feldstärketensor, Am: Viererpotential).
:
Feldstärketensor, Am: Viererpotential).
Im Minkowski-Raum mit ebener Metrik hmn haben die Maxwell-Gleichungen die Form:
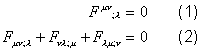
(kovariante Formulierung der Elektrodynamik). Das Index-Symbol
";l"
bezeichnet die kovariante Ableitung nach der Koordinate l bezüglich hmn.
In Inertialsystemen ist diese gleich der gewöhnlichen Ableitung ![]() . Beim Übergang
in einen Raum mit Gravitation (Riemannsche Mannigfaltigkeit) wird hmn
durch die das Graviationsfeld beschreibende Metrik gmn
ersetzt. In (2) muss ausserdem die kovariante Ableitung nach hmn
durch die nach gmn ersetzt werden. Aus den
Einstein-Gleichungen
. Beim Übergang
in einen Raum mit Gravitation (Riemannsche Mannigfaltigkeit) wird hmn
durch die das Graviationsfeld beschreibende Metrik gmn
ersetzt. In (2) muss ausserdem die kovariante Ableitung nach hmn
durch die nach gmn ersetzt werden. Aus den
Einstein-Gleichungen
![]() (3)
(3)
(Rmn: Ricci-Tensor, k = 8pG/c2: Einsteinsche Gravitationskonstante) ergeben sich dann mit (1) die Einstein-Maxwellschen Feldgleichungen:
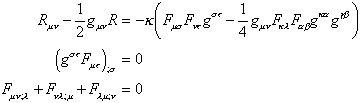
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.